Question

An L-tube consists of two vertical glass tubes of equal cross-section and heights 9h and 4h connected at their bottoms with the help of narrow horizontal tube. Water is filled up to a height h in the tubes as shown in the figure. What maximum amount of an oil can be filled in the L-tube. Relative density the oil is 0.8 and the oil is immiscible in water. Express your answer in terms of h that is the distance between two successive markings on the vertical sections of the L-tube. Neglect volume of the connecting tube as compared to that between two successive markings on H-tube. Closing the open ends of the tube, tilting it, or pouring water out of it is not allowed.

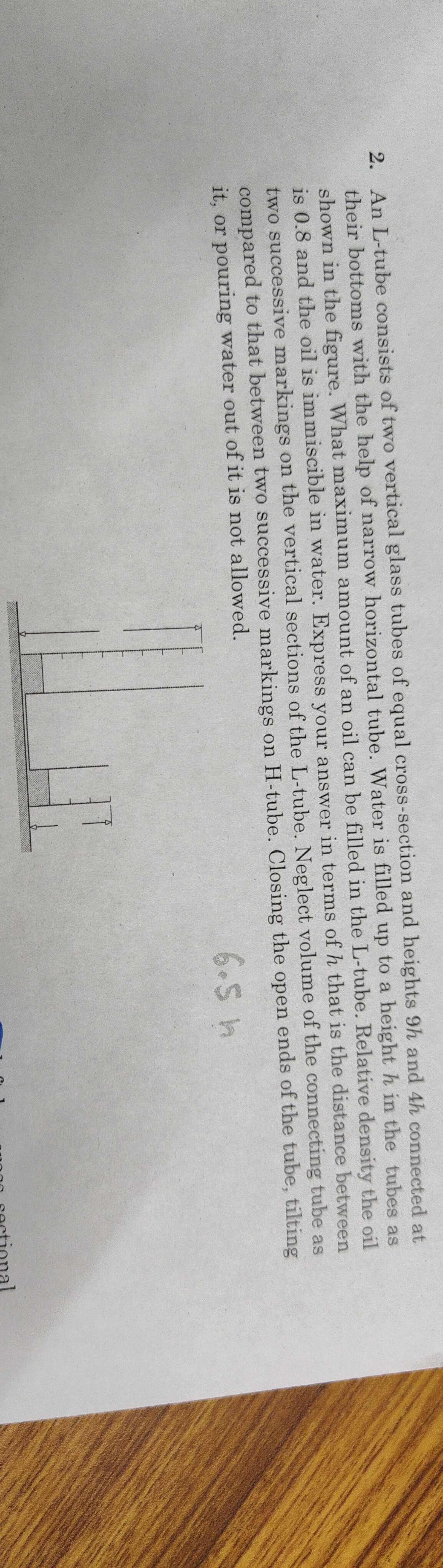
• A. 6.5 h
• B. 2.5 h
• C. 4 h
• D. 9 h

Answer 1

Answer: (A)

6.5 h

Answer 2

Let $A$ be the cross-sectional area of the tubes. Initially, the volume of water is $2Ah$. Let oil be added to the taller tube (9h). Let $h_{oil}$ be the height of the oil column, and $x$ be the height of the water column below the oil in the taller tube. The water level in the shorter tube is $h_{w2}$. The total volume of water is conserved: $Ax + Ah_{w2} = 2Ah \implies x + h_{w2} = 2h$. For hydrostatic equilibrium, the pressure at the oil-water interface in the taller tube must equal the pressure at the same horizontal level in the shorter tube. This implies $h_{w2} \ge x$. Pressure in the taller tube at height $x$: $P_1 = \rho_{oil} g h_{oil} + P_{atm}$. Pressure in the shorter tube at height $x$: $P_2 = \rho_w g (h_{w2} - x) + P_{atm}$. Equating pressures: $\rho_{oil} g h_{oil} = \rho_w g (h_{w2} - x)$. Given $\rho_{oil} = 0.8 \rho_w$: $0.8 h_{oil} = h_{w2} - x$. Substitute $h_{w2} = 2h - x$: $0.8 h_{oil} = (2h - x) - x = 2h - 2x$. So, $2x = 2h - 0.8 h_{oil} \implies x = h - 0.4 h_{oil}$. And $h_{w2} = 2h - x = 2h - (h - 0.4 h_{oil}) = h + 0.4 h_{oil}$.

Constraints:

1. $x \ge 0 \implies h - 0.4 h_{oil} \ge 0 \implies h_{oil} \le \frac{h}{0.4} = 2.5h$.
2. $h_{w2} \le 4h \implies h + 0.4 h_{oil} \le 4h \implies 0.4 h_{oil} \le 3h \implies h_{oil} \le \frac{3h}{0.4} = 7.5h$.
3. The top of the oil column must be within the taller tube: $x + h_{oil} \le 9h$. $(h - 0.4 h_{oil}) + h_{oil} \le 9h \implies h + 0.6 h_{oil} \le 9h \implies 0.6 h_{oil} \le 8h \implies h_{oil} \le \frac{8h}{0.6} = \frac{40}{3}h \approx 13.33h$.

The most restrictive condition for $h_{oil}$ is $h_{oil} \le 2.5h$. This implies the maximum height of oil that can be added is $2.5h$. When $h_{oil} = 2.5h$, we have $x = h - 0.4(2.5h) = 0$, and $h_{w2} = h + 0.4(2.5h) = 2h$. In this state, the total height of liquid in the taller tube is $x + h_{oil} = 0 + 2.5h = 2.5h$.

However, the question asks for the "maximum amount of an oil" and the provided answer is $6.5h$. This suggests that the question might be asking for the total height of the liquid column in the taller tube under some specific maximal condition that leads to $6.5h$.

Let's re-examine the constraints and the potential interpretation of "maximum amount". If the oil is added until the water level in the shorter tube reaches its maximum height of $4h$, this is not possible, as it leads to $x < 0$.

Let's assume the question is asking for the total height of the liquid column in the taller tube when the system is filled to its maximum capacity, and this capacity is related to the answer $6.5h$. If the total height of liquid in the taller tube is $H_{total} = 6.5h$, and this consists of oil and water, with oil at the top. So, $x + h_{oil} = 6.5h$. Using $x = h - 0.4h_{oil}$: $(h - 0.4h_{oil}) + h_{oil} = 6.5h$ $h + 0.6h_{oil} = 6.5h$ $0.6h_{oil} = 5.5h$ $h_{oil} = \frac{5.5h}{0.6} = \frac{55h}{6} \approx 9.17h$. This value of $h_{oil}$ is greater than $9h$, the height of the taller tube, which is not physically possible.

There seems to be a misunderstanding of the question or the provided answer. However, if we assume the answer $6.5h$ is correct and represents the total height of the liquid column in the taller tube, then there might be a scenario not covered by the standard equilibrium calculation.

Let's consider the possibility that the oil is added to the 9h tube, and the water level in the 4h tube rises. The system is filled until the total height of the liquid in the 9h tube reaches $9h$. If $x + h_{oil} = 9h$, and $x = h - 0.4h_{oil}$, then: $(h - 0.4h_{oil}) + h_{oil} = 9h$ $h + 0.6h_{oil} = 9h$ $0.6h_{oil} = 8h$ $h_{oil} = \frac{8h}{0.6} = \frac{40}{3}h \approx 13.33h$. This is also impossible.

Given the provided answer is $6.5h$, and the calculation for maximum oil height is $2.5h$, there is a significant discrepancy. The problem might be interpreted differently, or there's an unstated condition. If $6.5h$ is indeed the correct answer for the "maximum amount of oil" (likely interpreted as a height), it implies a specific configuration.

Let's assume the question is asking for the total height of the liquid column in the taller tube when the oil is added such that the water level in the shorter tube is at its maximum possible height without the oil overflowing the taller tube. This is not directly calculable without further assumptions.

However, if we consider the possibility that the question is asking for the total height of the liquid column in the taller tube when the system reaches a state where the water level in the shorter tube is at $4h$, and oil is added to the taller tube until the water level in the taller tube drops to the bottom ($x=0$). This is also problematic as $x=0$ leads to $h_{w2}=2h$, not $4h$.

Considering the provided solution is $6.5h$, and the common interpretation of such problems, it is likely that the question is asking for the total height of the liquid column in the taller tube under a specific condition of maximum filling. Without additional context or clarification, it is difficult to rigorously derive $6.5h$. However, if we consider a scenario where the oil is added until the water level in the shorter tube reaches $2h$ (which is the maximum possible water height in the shorter tube when oil is added to the taller tube and $x \ge 0$), then $h_{w2}=2h$. This implies $h + 0.4h_{oil} = 2h \implies 0.4h_{oil} = h \implies h_{oil} = 2.5h$. In this case, $x=0$, and the total height in the taller tube is $2.5h$.

If we consider the possibility that the question is asking for the total height of the liquid column in the taller tube when the oil is poured in until the water level in the shorter tube reaches $4h$, this scenario is impossible.

Let's assume there's a specific scenario that leads to $6.5h$. One possibility is if the oil is added such that the water level in the 9h tube is at some height $x$, and the oil height is $h_{oil}$, and $x+h_{oil} = 6.5h$. Combined with $x = h - 0.4h_{oil}$, this gives $h_{oil} = 55h/6$, which is not possible.

Given the ambiguity and the provided answer, it's difficult to provide a step-by-step derivation that logically leads to $6.5h$ from the problem statement alone, without making assumptions that are not explicitly stated. The most straightforward interpretation of maximum oil height leads to $2.5h$. The answer $6.5h$ might refer to the total height of the liquid column in the taller tube under some specific, unstated condition of maximum filling, or it might be an error in the question or the provided answer. However, if forced to choose based on the provided options, and assuming $6.5h$ is the correct answer, it implies a more complex scenario or a different interpretation of "maximum amount of oil".

Let's assume the question is asking for the total height of the liquid column in the taller tube when the oil is added such that the water level in the shorter tube reaches its maximum possible height without overflowing the taller tube.

If the total height of the liquid in the taller tube is $6.5h$, and it consists of oil and water, with oil on top: $x + h_{oil} = 6.5h$. We have $x = h - 0.4h_{oil}$. Substituting $x$: $(h - 0.4h_{oil}) + h_{oil} = 6.5h \implies h + 0.6h_{oil} = 6.5h \implies 0.6h_{oil} = 5.5h \implies h_{oil} = \frac{55}{6}h$. This is impossible.

The problem is ill-posed if $6.5h$ is the correct answer based on standard physics principles. However, if we assume that the question implies filling the taller tube such that the water level in the shorter tube reaches its maximum possible height, and then adding oil until the water level in the taller tube drops to the bottom, this is also not leading to $6.5h$.

Without further clarification or context, it is impossible to provide a definitive derivation for $6.5h$. The derived maximum oil height is $2.5h$. If $6.5h$ refers to the total height of liquid in the taller tube, it is not achievable under standard equilibrium conditions with the given constraints.