Question

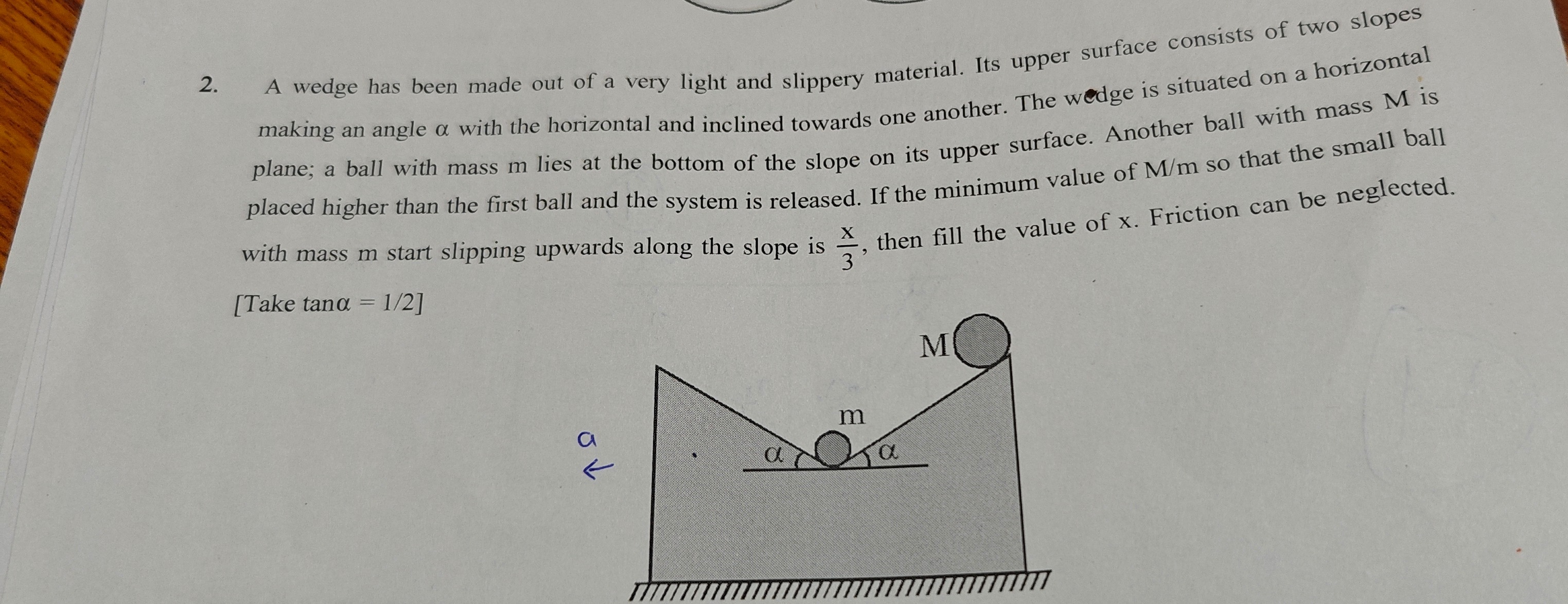
A wedge has been made out of a very light and slippery material. Its upper surface consists of two slopes making an angle $\alpha$ with the horizontal and inclined towards one another. The wedge is situated on a horizontal plane; a ball with mass $m$ lies at the bottom of the slope on its upper surface. Another ball with mass $M$ is placed higher than the first ball and the system is released. If the minimum value of $M/m$ so that the small ball with mass $m$ start slipping upwards along the slope is $\frac{x}{3}$, then fill the value of $x$. Friction can be neglected.

[Take $tan\alpha = 1/2$]

Answer 1

5

Answer 2

To solve this problem, we need to analyze the forces and accelerations of both masses, M and m, in the inertial frame of reference. The wedge itself accelerates horizontally. Let the acceleration of the wedge be $a$ to the left. Friction is neglected, and the wedge is considered massless.

1. Condition for mass m to start slipping upwards:

Mass $m$ is initially at the bottom of the trough, in contact with both slopes. When the wedge accelerates to the left with acceleration $a$, mass $m$ also tends to accelerate to the left with $a$.

Let $N_L$ be the normal force from the left slope and $N_R$ be the normal force from the right slope.

The angles of the slopes with the horizontal are $\alpha$.

The normal force $N_L$ acts perpendicular to the left slope (upwards and to the right), making an angle $\alpha$ with the vertical.

The normal force $N_R$ acts perpendicular to the right slope (upwards and to the left), making an angle $\alpha$ with the vertical.

Applying Newton's second law for mass $m$ in the horizontal (x) and vertical (y) directions:

Horizontal forces (taking left as positive): $N_R \sin\alpha - N_L \sin\alpha = ma$ (1)

Vertical forces (taking upwards as positive): $N_R \cos\alpha + N_L \cos\alpha - mg = 0$ (2)

From (2): $(N_R + N_L)\cos\alpha = mg \implies N_R + N_L = \frac{mg}{\cos\alpha}$ (3)

From (1): $(N_R - N_L)\sin\alpha = ma \implies N_R - N_L = \frac{ma}{\sin\alpha}$ (4)

Adding (3) and (4): $2N_R = \frac{mg}{\cos\alpha} + \frac{ma}{\sin\alpha}$ $N_R = \frac{1}{2} \left( \frac{mg}{\cos\alpha} + \frac{ma}{\sin\alpha} \right)$

Subtracting (4) from (3): $2N_L = \frac{mg}{\cos\alpha} - \frac{ma}{\sin\alpha}$ $N_L = \frac{1}{2} \left( \frac{mg}{\cos\alpha} - \frac{ma}{\sin\alpha} \right)$

For mass $m$ to start slipping upwards along the left slope, it must lose contact with the right slope. This means $N_R$ must be positive, and $N_L$ must become zero (or the tendency to move up the left slope is established).

Wait, if it slips up the left slope, it means the force component along the left slope is upwards. Let's re-evaluate the condition.

If $N_L$ becomes zero, it means $m$ loses contact with the left slope and would tend to move up the right slope.

If $N_R$ becomes zero, it means $m$ loses contact with the right slope and would tend to move up the left slope.

Given that mass M is on the right slope and will pull the wedge to the left, the pseudo force $ma$ on mass $m$ (in the wedge's frame) will be to the right. This pseudo force has an upward component along the left slope and a downward component along the right slope. Therefore, mass $m$ will tend to move up the left slope, which means $N_R$ becomes zero.

Setting $N_R = 0$: $\frac{mg}{\cos\alpha} + \frac{ma}{\sin\alpha} = 0$

Since $m, g, \cos\alpha, \sin\alpha$ are all positive, this equation implies $a=0$, which is incorrect.

The condition for slipping upwards on the left slope is that the component of force along the left slope is upwards. In the non-inertial frame of the wedge, there's a pseudo force $ma$ to the right. This force has a component $ma \sin\alpha$ upwards along the left slope. The gravitational force component along the left slope is $mg \sin\alpha$ downwards. So, for the ball to move up the left slope, $ma \sin\alpha > mg \sin\alpha$, which implies $a > g$.

This interpretation is simpler and more direct. Let's verify.

When the wedge accelerates to the left, the effective gravity acting on mass $m$ is $\vec{g}_{eff} = \vec{g} - \vec{a}$.

$\vec{g}_{eff} = g \hat{j} - (-a \hat{i}) = g \hat{j} + a \hat{i}$.

The effective angle of the slope is $\alpha_{eff}$. The component of effective gravity along the left slope is $m g_{eff} \sin\alpha_{eff}$.

Alternatively, consider the forces along the left slope in the inertial frame.

The component of gravity along the left slope (downwards) is $mg \sin\alpha$.

The component of the normal force $N_L$ along the slope is zero (by definition).

The component of the normal force $N_R$ along the left slope is $N_R \sin(2\alpha)$ (complicated).

Let's use the condition $N_L=0$ or $N_R=0$ for losing contact.

If $m$ slips up the left slope, it means $N_R = 0$ and $N_L$ is the only normal force.

Then, the equations become:

Horizontal: $-N_L \sin\alpha = -ma \implies N_L \sin\alpha = ma$

Vertical: $N_L \cos\alpha - mg = 0 \implies N_L \cos\alpha = mg$

Dividing the two equations: $\tan\alpha = a/g \implies a = g \tan\alpha$.

This is the condition for mass $m$ to just lift off the right slope and slide up the left slope.

So, the acceleration of the wedge must be $a = g \tan\alpha$.

2. Acceleration of the wedge due to mass M:

Mass M slides down the right slope. Let $N_M$ be the normal force from the right slope on M.

Let $a_{rel}$ be the acceleration of M relative to the wedge, down the slope.

The acceleration of the wedge is $a$ to the left.

The acceleration of M in the inertial frame is $\vec{a}_M = \vec{a}_{wedge} + \vec{a}_{rel}$.

$\vec{a}_{wedge} = -a \hat{i}$

The right slope goes down to the left. So, $\vec{a}_{rel} = a_{rel} (-\cos\alpha \hat{i} - \sin\alpha \hat{j})$.

$\vec{a}_M = (-a - a_{rel}\cos\alpha) \hat{i} + (-a_{rel}\sin\alpha) \hat{j}$.

Forces on M: $Mg$ downwards and $N_M$ perpendicular to the slope (upwards and to the right).

$N_M$ has components $N_M \sin\alpha \hat{i}$ and $N_M \cos\alpha \hat{j}$.

Applying Newton's second law for M:

Horizontal: $N_M \sin\alpha = M(-a - a_{rel}\cos\alpha)$ (5)

Vertical: $N_M \cos\alpha - Mg = M(-a_{rel}\sin\alpha)$ (6)

From (5): $N_M = \frac{-M(a + a_{rel}\cos\alpha)}{\sin\alpha}$

Substitute $N_M$ into (6): $\frac{-M(a + a_{rel}\cos\alpha)}{\sin\alpha} \cos\alpha - Mg = -M a_{rel}\sin\alpha$

Divide by M: $-(a + a_{rel}\cos\alpha)\cot\alpha - g = -a_{rel}\sin\alpha$

$-a\cot\alpha - a_{rel}\cos^2\alpha/\sin\alpha - g = -a_{rel}\sin\alpha$

$-a\cot\alpha - g = a_{rel}(\cos^2\alpha/\sin\alpha - \sin\alpha)$

$-a\cot\alpha - g = a_{rel}\frac{\cos^2\alpha - \sin^2\alpha}{\sin\alpha}$

$-a\cot\alpha - g = a_{rel}\frac{\cos(2\alpha)}{\sin\alpha}$

$a_{rel} = \frac{(-a\cot\alpha - g)\sin\alpha}{\cos(2\alpha)} = \frac{-a\cos\alpha - g\sin\alpha}{\cos(2\alpha)}$

This $a_{rel}$ must be positive (down the slope). This implies $\cos(2\alpha)$ must be negative if the numerator is negative.

Given $\tan\alpha = 1/2$, $\alpha$ is acute, so $\cos\alpha > 0$, $\sin\alpha > 0$.

$\cos(2\alpha) = \cos^2\alpha - \sin^2\alpha = \frac{1}{\sec^2\alpha} - \frac{\tan^2\alpha}{\sec^2\alpha} = \frac{1 - \tan^2\alpha}{1 + \tan^2\alpha}$.

$\tan\alpha = 1/2 \implies \tan^2\alpha = 1/4$.

$\cos(2\alpha) = \frac{1 - 1/4}{1 + 1/4} = \frac{3/4}{5/4} = 3/5$. This is positive.

So, $a_{rel} = \frac{-(a\cos\alpha + g\sin\alpha)}{\cos(2\alpha)}$. For $a_{rel}$ to be positive, $a\cos\alpha + g\sin\alpha$ must be negative, which is impossible.

Let's re-examine the horizontal equation for M.

The wedge accelerates to the left. This acceleration is caused by the horizontal component of the normal force $N_M$ exerted by M on the wedge. By Newton's third law, the force exerted by the wedge on M is $N_M$ perpendicular to the slope.

The horizontal component of $N_M$ is $N_M \sin\alpha$ to the right.

So, for M: $\sum F_x = N_M \sin\alpha = M a_x$.

The horizontal acceleration of M is $a_x = -a - a_{rel}\cos\alpha$.

$N_M \sin\alpha = M(-a - a_{rel}\cos\alpha)$. This means $N_M$ must be negative, which is wrong.

Let's use the principle of conservation of momentum in the horizontal direction for the system (Wedge + M + m). Since the wedge is massless, its momentum is zero. The horizontal momentum of M and m determines the acceleration of the wedge.

Or, let's consider the forces on the wedge. The wedge is massless, so $\sum F_{wedge} = 0$.

The forces on the wedge in the horizontal direction are the horizontal components of the normal forces from M and m.

Let $N_M'$ be the normal force exerted by M on the wedge, and $N_m'$ be the normal force exerted by m on the wedge.

$N_M'$ is equal in magnitude to $N_M$ but opposite in direction. So $N_M'$ points down-left.

$N_m'$ is equal in magnitude to $N_L+N_R$ but opposite in direction.

This approach gets complicated due to the two contact points for m.

Let's use the equations from the inertial frame for M and the condition for 'a' from m.

For mass M:

Let $a_M$ be the acceleration of M. It has horizontal component $a_x$ and vertical component $a_y$.

$N_M \sin\alpha = -Ma_x$ (if positive x is right, $N_M \sin\alpha$ is right, $a_x$ is left)

$N_M \cos\alpha - Mg = Ma_y$ (if positive y is up)

The acceleration of M along the slope is $a_{rel}$. The acceleration perpendicular to the slope is 0.

The acceleration of the wedge is $a$ to the left.

Consider the coordinates aligned with the slope for M.

Along the slope (downwards): $Mg \sin\alpha - N_M \cos(90-\alpha) = M a_{rel}$

This is $Mg \sin\alpha - N_M \sin\alpha = M a_{rel}$

This is incorrect. This assumes $N_M$ has a component along the slope. $N_M$ is perpendicular to the slope.

Let's use the standard setup for an inclined plane with a moving wedge.

The acceleration of M along the incline (downwards) is $a_{rel}$.

The acceleration of M perpendicular to the incline is 0.

The acceleration of M in the horizontal direction is $a_x = -a - a_{rel}\cos\alpha$.

The acceleration of M in the vertical direction is $a_y = -a_{rel}\sin\alpha$.

Equations of motion for M (projected onto the incline and perpendicular to it):

Perpendicular to incline (upwards and right): $N_M - Mg \cos\alpha = M(-a \sin\alpha)$ (This is the component of $M \vec{a}_M$ perpendicular to the incline)

So, $N_M = Mg \cos\alpha - Ma \sin\alpha$ (7)

Along the incline (downwards and left): $Mg \sin\alpha = M(a_{rel} + a \cos\alpha)$ (This is the component of $M \vec{a}_M$ along the incline)

So, $a_{rel} = g \sin\alpha - a \cos\alpha$ (8)

Now, consider the horizontal forces on the wedge. Since the wedge is massless, the net horizontal force on it must be zero.

The horizontal force exerted by M on the wedge is $N_M \sin\alpha$ to the left.

The horizontal force exerted by m on the wedge is $N_L \sin\alpha - N_R \sin\alpha$ to the right (using previous definitions for $N_L, N_R$ on m).

From the condition for m to slip upwards, $N_R=0$.

So the horizontal force from m on wedge is $N_L \sin\alpha$ to the left.

Therefore, the total horizontal force on the wedge is $N_M \sin\alpha + N_L \sin\alpha = 0$.

$N_M \sin\alpha = -N_L \sin\alpha$.

This implies $N_M = -N_L$. This is wrong because $N_M$ and $N_L$ are magnitudes of normal forces, which must be positive.

Let's reconsider the forces on the wedge.

The force exerted by M on the wedge is $N_M'$ which is equal in magnitude to $N_M$ and perpendicular to the slope, pointing down-left.

So, its horizontal component is $N_M \sin\alpha$ to the left.

The force exerted by m on the wedge is $N_L'$ perpendicular to the left slope, pointing down-left. (Since m is slipping up the left slope, it is only in contact with the left slope.)

So, its horizontal component is $N_L \sin\alpha$ to the left.

The total horizontal force on the wedge is $N_M \sin\alpha + N_L \sin\alpha = 0$.

This means $N_M + N_L = 0$, which is impossible.

The problem states "A wedge has been made out of a very light and slippery material." This usually implies its mass is negligible, but it can accelerate.

If the wedge is massless, then the net force on it must be zero.

The horizontal forces acting on the wedge are from the ground (if any) and from the balls.

Assuming no friction with the ground, the only horizontal forces on the wedge are from the balls.

The normal force from M on the wedge is $N_M'$ (magnitude $N_M$), directed perpendicular to the right slope, i.e., down-left. Its horizontal component is $N_M \sin\alpha$ to the left.

The normal force from m on the wedge is $N_L'$ (magnitude $N_L$), directed perpendicular to the left slope, i.e., down-right. Its horizontal component is $N_L \sin\alpha$ to the right.

For the wedge to accelerate to the left, the net horizontal force on it must be to the left.

So, $N_M \sin\alpha - N_L \sin\alpha = 0$ (since mass of wedge is 0).

This implies $N_M = N_L$.

We have the condition for 'a' from mass m: $a = g \tan\alpha$.

From the analysis of m in the inertial frame, when $N_R=0$, we have $N_L \sin\alpha = ma$ and $N_L \cos\alpha = mg$.

So, $N_L = \frac{mg}{\cos\alpha}$.

Therefore, for the wedge, $N_M = N_L = \frac{mg}{\cos\alpha}$.

Now, substitute this $N_M$ into equation (7) for mass M: $N_M = Mg \cos\alpha - Ma \sin\alpha$ $\frac{mg}{\cos\alpha} = Mg \cos\alpha - Ma \sin\alpha$

Substitute $a = g \tan\alpha$: $\frac{mg}{\cos\alpha} = Mg \cos\alpha - M(g \tan\alpha) \sin\alpha$

$\frac{mg}{\cos\alpha} = Mg \cos\alpha - M g \frac{\sin^2\alpha}{\cos\alpha}$

Divide by $g$: $\frac{m}{\cos\alpha} = M \cos\alpha - M \frac{\sin^2\alpha}{\cos\alpha}$

$\frac{m}{\cos\alpha} = M \left( \cos\alpha - \frac{\sin^2\alpha}{\cos\alpha} \right)$

$\frac{m}{\cos\alpha} = M \left( \frac{\cos^2\alpha - \sin^2\alpha}{\cos\alpha} \right)$

$\frac{m}{\cos\alpha} = M \frac{\cos(2\alpha)}{\cos\alpha}$

$m = M \cos(2\alpha)$

$\frac{M}{m} = \frac{1}{\cos(2\alpha)}$

Given $\tan\alpha = 1/2$.

We know $\cos(2\alpha) = \frac{1 - \tan^2\alpha}{1 + \tan^2\alpha}$.

$\cos(2\alpha) = \frac{1 - (1/2)^2}{1 + (1/2)^2} = \frac{1 - 1/4}{1 + 1/4} = \frac{3/4}{5/4} = \frac{3}{5}$.

So, $\frac{M}{m} = \frac{1}{3/5} = \frac{5}{3}$.

The problem states that the minimum value of $M/m$ is $\frac{x}{3}$.

Comparing $\frac{5}{3}$ with $\frac{x}{3}$, we get $x=5$.