Solveeit Logo
Login

Question

Question: A weak base BOH was titrated against a strong acid. The pH at 1/4th equivalence point was 8.0. Enoug...

A weak base BOH was titrated against a strong acid. The pH at 1/4th equivalence point was 8.0. Enough strong base was now added (7.5 millimole) to completely convert the salt. The total volume was 10 ml. Find the pOH at this point.

Answer

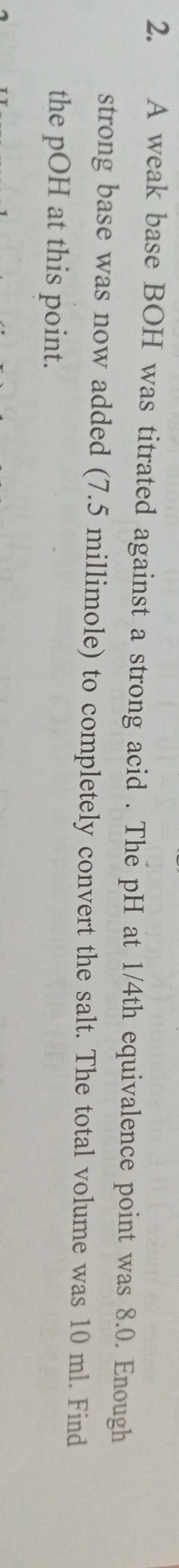
3.301

Explanation

Solution

Let the weak base be BOH and the strong acid be HA. The titration reaction is BOH + HA →\rightarrow BA + H2_2O.
Let the initial number of millimoles of BOH be n0n_0.

At 1/4th equivalence point, 1/4th of the initial weak base has been neutralized by the strong acid.
Millimoles of HA added = n0/4n_0/4.
Millimoles of BOH remaining = n0−n0/4=3n0/4n_0 - n_0/4 = 3n_0/4.
Millimoles of salt BA formed = n0/4n_0/4.

At this point, the solution is a buffer containing the weak base BOH and its salt BA.
The pH at this point is given as 8.0.
The pOH is 14−pH=14−8.0=6.014 - \text{pH} = 14 - 8.0 = 6.0.

For a basic buffer, the Henderson-Hasselbalch equation is pOH = pKb_b + log [Salt][Base]\frac{\text{[Salt]}}{\text{[Base]}}.
Since the salt and base are in the same volume, the ratio of concentrations is equal to the ratio of millimoles.
pOH = pKb_b + log moles of BAmoles of BOH\frac{\text{moles of BA}}{\text{moles of BOH}}
6.0=pKb+logn0/43n0/46.0 = \text{pK}_b + \text{log} \frac{n_0/4}{3n_0/4}
6.0=pKb+log(1/3)6.0 = \text{pK}_b + \text{log}(1/3)
6.0=pKb−log(3)6.0 = \text{pK}_b - \text{log}(3)
pKb=6.0+log(3)_b = 6.0 + \text{log}(3).

Next, "Enough strong base was now added (7.5 millimole) to completely convert the salt". This implies that the amount of salt present before adding the strong base was 7.5 millimole. The salt BA is formed during the titration of BOH with HA. The maximum amount of salt BA is formed at the equivalence point, where all the initial BOH is converted to BA. Therefore, the amount of salt present at the equivalence point is equal to the initial amount of weak base, n0n_0.
So, the amount of salt BA that was present and needed to be converted is 7.5 millimole. This means the initial amount of weak base BOH was n0=7.5n_0 = 7.5 millimole.

The salt BA reacts with a strong base (OH−^-) to form the weak base BOH:
BA + OH−^- →\rightarrow BOH + A−^- (or more precisely, B+^+ + OH−^- →\rightarrow BOH).
To completely convert 7.5 millimole of salt BA, 7.5 millimole of strong base is required. The problem states that 7.5 millimole of strong base was added to completely convert the salt. This confirms that the amount of salt present was 7.5 millimole, which means the process started from the equivalence point of the initial titration, where 7.5 millimole of BA was present.

So, we start with 7.5 millimole of salt BA and add 7.5 millimole of strong base (OH−^-).
Reaction: B+^+ + OH−^- →\rightarrow BOH
Initial: 7.5 mmol 7.5 mmol 0
Change: -7.5 mmol -7.5 mmol +7.5 mmol
Final: 0 mmol 0 mmol 7.5 mmol

After the addition of the strong base, the solution contains 7.5 millimole of the weak base BOH.
The total volume of the solution at this point is given as 10 ml.
The concentration of BOH is [BOH] = molesvolume=7.5 mmol10 ml=0.75 M\frac{\text{moles}}{\text{volume}} = \frac{7.5 \text{ mmol}}{10 \text{ ml}} = 0.75 \text{ M}.

Now we need to find the pOH of a 0.75 M solution of the weak base BOH.
BOH ⇌\rightleftharpoons B+^+ + OH−^-
The base dissociation constant Kb_b is related to pKb_b by Kb=10−pKb_b = 10^{-\text{pK}_b}.
pKb=6+log(3)_b = 6 + \text{log}(3).
Kb=10−(6+log(3))=10−6×10−log(3)=10−6×13_b = 10^{-(6 + \text{log}(3))} = 10^{-6} \times 10^{-\text{log}(3)} = 10^{-6} \times \frac{1}{3}.
Kb=13×10−6_b = \frac{1}{3} \times 10^{-6}.

Let x be the concentration of OH−^- ions at equilibrium.
BOH ⇌\rightleftharpoons B+^+ + OH−^-
Initial: 0.75 M 0 0
Change: -x +x +x
Equilibrium: 0.75-x M x M x M

Kb=[B+][OH−][BOH]=x×x0.75−x=x20.75−x_b = \frac{\text{[B}^+][\text{OH}^-]}{\text{[BOH]}} = \frac{x \times x}{0.75 - x} = \frac{x^2}{0.75 - x}.
Assuming x is much smaller than 0.75 (since Kb_b is small), we can approximate 0.75 - x ≈\approx 0.75.
Kb≈x20.75_b \approx \frac{x^2}{0.75}
x2=Kb×0.75=13×10−6×0.75=13×10−6×34=14×10−6x^2 = \text{K}_b \times 0.75 = \frac{1}{3} \times 10^{-6} \times 0.75 = \frac{1}{3} \times 10^{-6} \times \frac{3}{4} = \frac{1}{4} \times 10^{-6}.
x=14×10−6=12×10−3=0.5×10−3=5×10−4x = \sqrt{\frac{1}{4} \times 10^{-6}} = \frac{1}{2} \times 10^{-3} = 0.5 \times 10^{-3} = 5 \times 10^{-4} M.
[OH−^-] = 5×10−45 \times 10^{-4} M.
Checking the assumption: x=5×10−4x = 5 \times 10^{-4} M is indeed much smaller than 0.75 M.

Now calculate pOH:
pOH = -log[OH−^-] = -log(5×10−45 \times 10^{-4})
pOH = - (log(5) + log(10−410^{-4}))
pOH = - (log(5) - 4)
pOH = 4 - log(5).
Using log(5) ≈\approx 0.699:
pOH = 4 - 0.699 = 3.301.