Question
Question: A straight rod of length $\ell$ extends from x = $\alpha$ to x = $\ell$ + $\alpha$ as shown in the f...
A straight rod of length ℓ extends from x = α to x = ℓ + α as shown in the figure. If the mass per unit length is (a + bx²). The gravitational force it exerts on a point mass m placed at x = 0 is given by
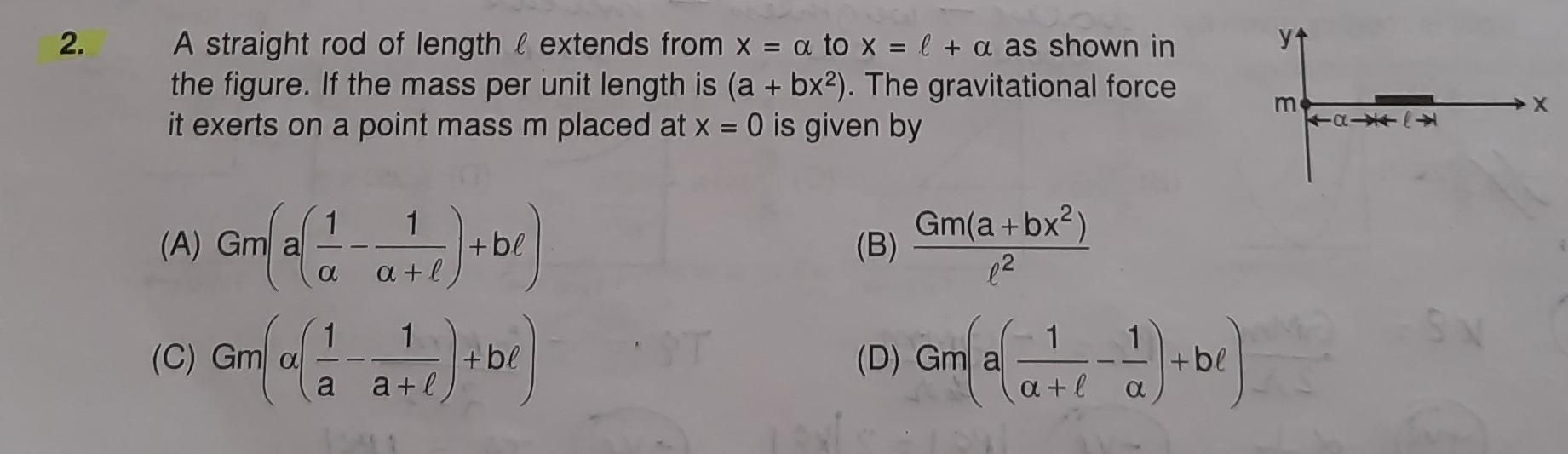
Gm(a(α1−α+ℓ1)+bℓ)
ℓ2Gm(a+bx2)
Gm(α(a1−a+ℓ1)+bℓ)
Gm(a(α+ℓ1−α1)+bℓ)
A
Solution
The gravitational force exerted by a continuous mass distribution is found by integrating the differential force exerted by a small mass element.
-
Define a differential mass element:
Consider a small element of the rod of length dx at a distance x from the origin (where the point mass m is placed).
The mass per unit length is given as λ=(a+bx2).
The mass of this differential element dm is λdx=(a+bx2)dx. -
Calculate the differential gravitational force:
The gravitational force dF exerted by this element dm on the point mass m at x=0 is given by Newton's law of gravitation: dF=x2Gm⋅dm Substitute the expression for dm: dF=x2Gm(a+bx2)dx -
Integrate to find the total force:
The rod extends from x=α to x=ℓ+α. To find the total gravitational force F, integrate dF over these limits: F=∫αℓ+αx2Gm(a+bx2)dx Since G and m are constants, they can be taken out of the integral: F=Gm∫αℓ+α(x2a+x2bx2)dx F=Gm∫αℓ+α(ax−2+b)dx -
Perform the integration:
The integral of ax−2 is −ax−1=−xa.
The integral of b is bx. F=Gm[−xa+bx]αℓ+α -
Apply the limits of integration: F=Gm[(−ℓ+αa+b(ℓ+α))−(−αa+bα)] F=Gm[−ℓ+αa+bℓ+bα+αa−bα] F=Gm[αa−ℓ+αa+bℓ] Factor out a from the first two terms: F=Gm[a(α1−ℓ+α1)+bℓ]
Comparing this result with the given options, it matches option (A).
