Question
Question: A solid cylinderical wire of radius 'R' carries a current T. The magnetic field is 5µT at a point, w...
A solid cylinderical wire of radius 'R' carries a current T. The magnetic field is 5µT at a point, which is '2R' distance away from the axis of wire. Magnetic field at a point which is R/3 distance inside from the surface of the wire is :-
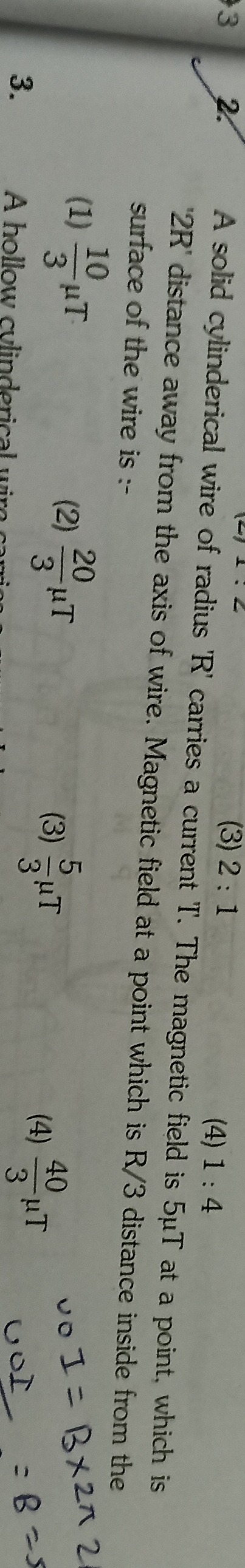
310µT
320µT
35µT
340µT
(2)
Solution
-
Formulas for Magnetic Field due to a Solid Cylindrical Wire:
For a solid cylindrical wire of radius 'R' carrying a current 'I':
-
Outside the wire (r > R): The magnetic field at a distance 'r' from the axis is given by: Boutside=2πrμ0I
-
Inside the wire (r < R): Assuming uniform current density, the magnetic field at a distance 'r' from the axis is given by: Binside=2πR2μ0Ir
-
-
Step 1: Use the given information to find the relationship between μ0I and R.
We are given that the magnetic field is 5 µT at a point 2R distance away from the axis. This point is outside the wire (since 2R > R).
Using the formula for Boutside:
5×10−6 T=2π(2R)μ0I
5×10−6=4πRμ0I
From this, we can express πRμ0I:
πRμ0I=4×(5×10−6)=20×10−6 T
-
Step 2: Determine the radial distance for the second point.
The point is R/3 distance inside from the surface of the wire.
The distance from the axis of the wire to the surface is R.
So, the distance from the axis to the point in question (let's call it r') is:
r′=R−3R=33R−R=32R
Since r′=32R<R, this point is indeed inside the wire.
-
Step 3: Calculate the magnetic field at the second point.
Using the formula for Binside:
Bnew=2πR2μ0Ir′
Substitute r′=32R:
Bnew=2πR2μ0I(2R/3)
Bnew=2πR2μ0I×32R
Bnew=3πRμ0I
-
Step 4: Substitute the value from Step 1 into the expression for Bnew.
We found πRμ0I=20×10−6 T.
So, Bnew=31×(πRμ0I)
Bnew=31×(20×10−6 T)
Bnew=320×10−6 T
Bnew=320μT
The magnetic field at a point which is R/3 distance inside from the surface of the wire is 320 µT.
