Question

A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of the liquid in the jar. Then the surface of the jar is a surface of revolution of the curve -

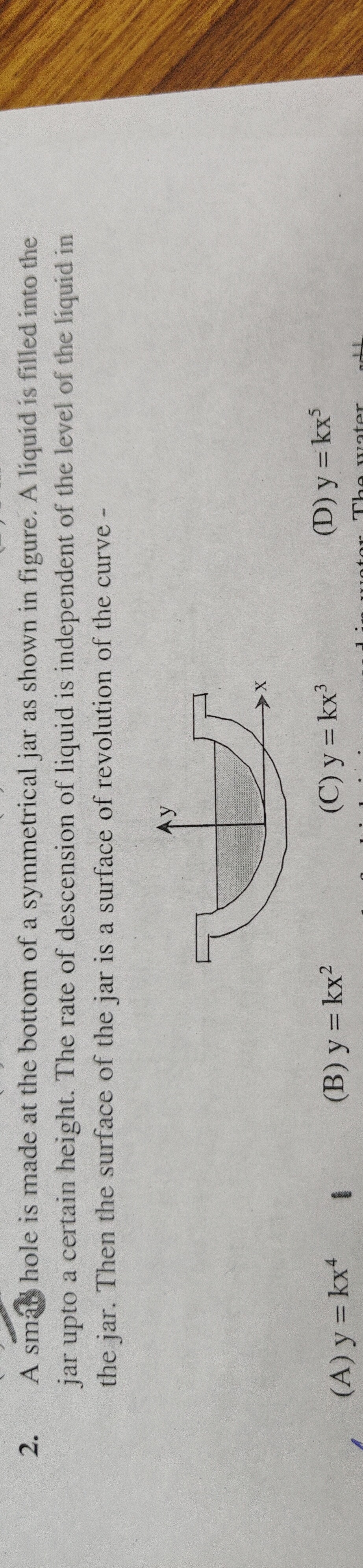
• A. y = kx⁴
• B. y = kx²
• C. y = kx³
• D. y = kx⁵

Answer 1

Answer: (A)

y = kx⁴

Answer 2

The volume $V$ of liquid in a jar formed by revolving the curve $y=kx^n$ about the y-axis, up to a height $h$, is proportional to $h^{1+2/n}$. The rate of change of volume with respect to height is $\frac{dV}{dh} \propto h^{2/n}$. According to Torricelli's Law, the rate of volume outflow through a hole at the bottom is $\frac{dV}{dt} \propto \sqrt{h}$. Using the chain rule, $\frac{dV}{dt} = \frac{dV}{dh} \frac{dh}{dt}$. Substituting the proportionalities, we get $h^{1/2} \propto h^{2/n} \frac{dh}{dt}$. For the rate of descent of the liquid level, $\frac{dh}{dt}$, to be independent of $h$, the exponent of $h$ on both sides of the proportionality must be equal: $1/2 = 2/n$. Solving this equation for $n$ yields $n=4$. Therefore, the curve is $y = kx^4$.