Question

A projectile of mass 'm' is thrown from the origin O with a velocity $v_0$ at an angle $\theta$. Identify the CORRECT statement :-

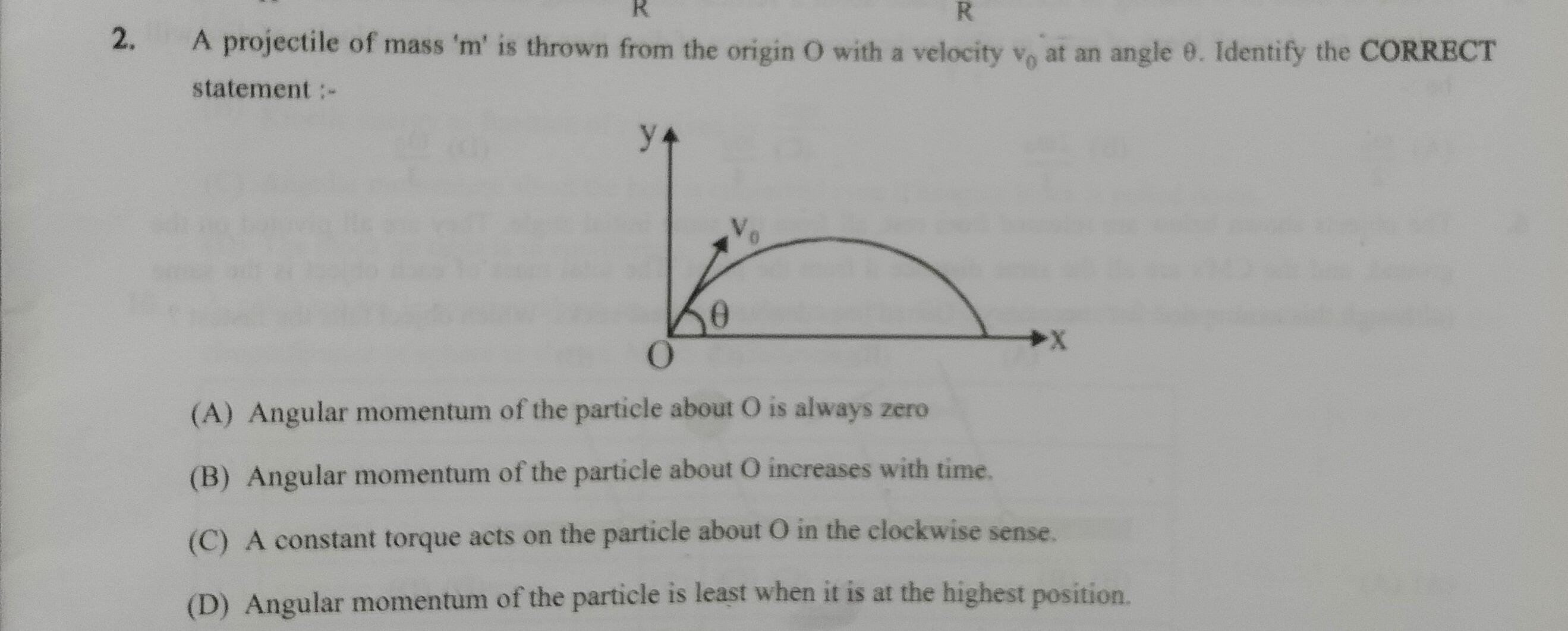
• A. Angular momentum of the particle about O is always zero
• B. Angular momentum of the particle about O increases with time.
• C. A constant torque acts on the particle about O in the clockwise sense.
• D. Angular momentum of the particle is least when it is at the highest position.

Answer 1

Answer: (B)

Angular momentum of the particle about O increases with time.

Answer 2

The angular momentum $\vec{L}$ of a particle about a point O is given by $\vec{L} = \vec{r} \times \vec{p}$, where $\vec{r}$ is the position vector from O and $\vec{p} = m\vec{v}$ is the linear momentum. The torque $\vec{\tau}$ about O is $\vec{\tau} = \vec{r} \times \vec{F}$. The rate of change of angular momentum is equal to the torque: $\frac{d\vec{L}}{dt} = \vec{\tau}$.

For projectile motion, the force is gravity, $\vec{F} = -mg\hat{j}$. The torque about the origin O is $\vec{\tau} = \vec{r} \times \vec{F} = -mgx\hat{k}$. Since $x(t) = (v_0 \cos\theta)t$, the torque is $\vec{\tau}(t) = -mg(v_0 \cos\theta)t\hat{k}$, which is not constant. Thus, statement (C) is incorrect.

Integrating the torque with respect to time gives the angular momentum: $\vec{L}(t) = \int \vec{\tau}(t) dt = -\frac{1}{2}mg(v_0 \cos\theta)t^2\hat{k} + \vec{C}$. Since $\vec{L}(0) = \vec{0}$, the constant of integration $\vec{C} = \vec{0}$. So, $\vec{L}(t) = -\frac{1}{2}mg(v_0 \cos\theta)t^2\hat{k}$.

(A) The angular momentum is zero only at $t=0$. For $t>0$, it is non-zero. Thus, statement (A) is incorrect. (B) The magnitude of angular momentum $|L_z(t)| = \frac{1}{2}mg(v_0 \cos\theta)t^2$. For $t>0$ and $0 < \theta < \pi/2$, this magnitude increases quadratically with time. Thus, statement (B) is correct. (D) The minimum angular momentum is 0 at $t=0$. The highest position is reached at $t_{top} = \frac{v_0 \sin\theta}{g}$, where the angular momentum is non-zero. Thus, statement (D) is incorrect.