Question
Question: A continuous function f: [0, 1) → [0, ∞) satisfies $f(\frac{x+1}{2})=f(x)+1$ and $f(1-x)=\frac{1}{f(...
A continuous function f: [0, 1) → [0, ∞) satisfies f(2x+1)=f(x)+1 and f(1−x)=f(x)1∀x∈(0,1).
Then TRUE Statement is/are
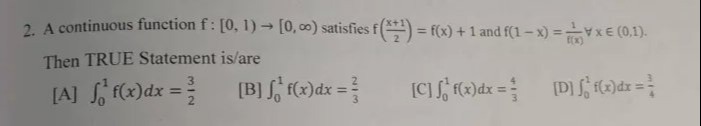
∫01f(x)dx=23
∫01f(x)dx=32
∫01f(x)dx=34
∫01f(x)dx=43
∫01f(x)dx=23
Solution
Let I=∫01f(x)dx. Using the property ∫0af(x)dx=∫0af(a−x)dx, we have I=∫01f(1−x)dx. Using the given condition f(1−x)=f(x)1, we get I=∫01f(x)1dx.
Split the integral I into two parts: I=∫01/2f(x)dx+∫1/21f(x)dx.
Consider the second integral ∫1/21f(x)dx. Let x=2y+1, so dx=21dy. When x=1/2, y=0. When x=1, y=1. ∫1/21f(x)dx=∫01f(2y+1)21dy. Using the condition f(2y+1)=f(y)+1: ∫1/21f(x)dx=∫01(f(y)+1)21dy=21∫01f(y)dy+21∫011dy=21I+21.
Substitute this back into the expression for I: I=∫01/2f(x)dx+(21I+21). This implies ∫01/2f(x)dx=21I−21.
Now consider the integral ∫01/2f(x)dx. Let x=1−u, so dx=−du. When x=0, u=1. When x=1/2, u=1/2. ∫01/2f(x)dx=∫11/2f(1−u)(−du)=∫1/21f(1−u)du. Using f(1−u)=1/f(u): ∫01/2f(x)dx=∫1/21f(u)1du.
So, 21I−21=∫1/21f(x)1dx.
We also have I=∫01f(x)1dx=∫01/2f(x)1dx+∫1/21f(x)1dx. Substitute the expression for ∫1/21f(x)1dx: I=∫01/2f(x)1dx+(21I−21). This implies ∫01/2f(x)1dx=21I+21.
We have the relations:
- ∫01/2f(x)dx=2I−21
- ∫1/21f(x)dx=2I+21
- ∫01/2f(x)1dx=2I+21
- ∫1/21f(x)1dx=2I−21
Consider the integral ∫01/2f(x)dx. Let x=2u, so dx=2du. ∫01/2f(x)dx=∫01f(2u)21du. So, 21∫01f(2u)du=2I−21. ∫01f(2u)du=I−1.
If we assume I=3/2, then ∫01f(2u)du=3/2−1=1/2. This is consistent with ∫01/2f(x)dx=23/2−21=43−21=41, and ∫1/21f(x)dx=23/2+21=43+21=45. And ∫01/2f(x)dx+∫1/21f(x)dx=41+45=46=23=I.
The value I=3/2 is consistent with the derived relations.
