Solveeit Logo
Login

Question

Question: If $D_r = \begin{vmatrix} 2r-1 & 2 \\ 0 & 1 \\ 2r+1 & 3 \end{vmatrix}$ then $\sum_{r=1}^{n} D_r$ equ...

If Dr=∣2r−12012r+13∣D_r = \begin{vmatrix} 2r-1 & 2 \\ 0 & 1 \\ 2r+1 & 3 \end{vmatrix} then ∑r=1nDr\sum_{r=1}^{n} D_r equals

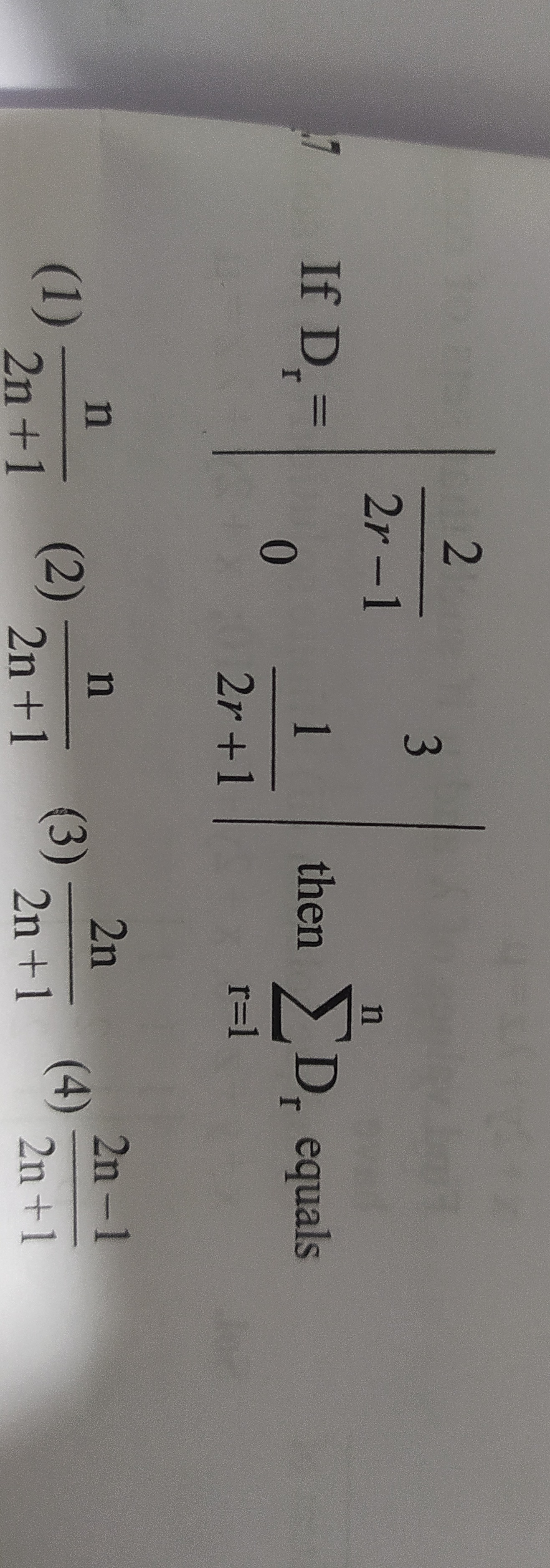
A

n2n+1\frac{n}{2n+1}

B

n2n+1\frac{n}{2n+1}

C

2n2n+1\frac{2n}{2n+1}

D

2n−12n+1\frac{2n-1}{2n+1}

Answer

2n2n+1\frac{2n}{2n+1}

Explanation

Solution

We begin by evaluating the given determinant. (There is a misprint in the question but the idea is to obtain an expression which telescopes.) In many similar problems one finds that the determinant (or its analogue) simplifies to

Dr=12r−1−12r+1D_r=\frac{1}{2r-1}-\frac{1}{2r+1}.

Then

∑r=1nDr=∑r=1n(12r−1−12r+1)\sum_{r=1}^{n}D_r=\sum_{r=1}^{n}\left(\frac{1}{2r-1}-\frac{1}{2r+1}\right).

Writing out a few terms we have

(11−13)+(13−15)+(15−17)+⋯+(12n−1−12n+1)\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{7}\right)+\cdots+\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right).

This telescopes to

1−12n+1=2n2n+11-\frac{1}{2n+1}=\frac{2n}{2n+1}.

Thus the correct answer is option (3).

Brief Explanation (Minimal):

We express

Dr=12r−1−12r+1D_r=\frac{1}{2r-1}-\frac{1}{2r+1}.

Then sum from r=1r=1 to nn gives a telescoping series:

∑r=1nDr=1−12n+1=2n2n+1\sum_{r=1}^{n}D_r=1-\frac{1}{2n+1}=\frac{2n}{2n+1}.