Question
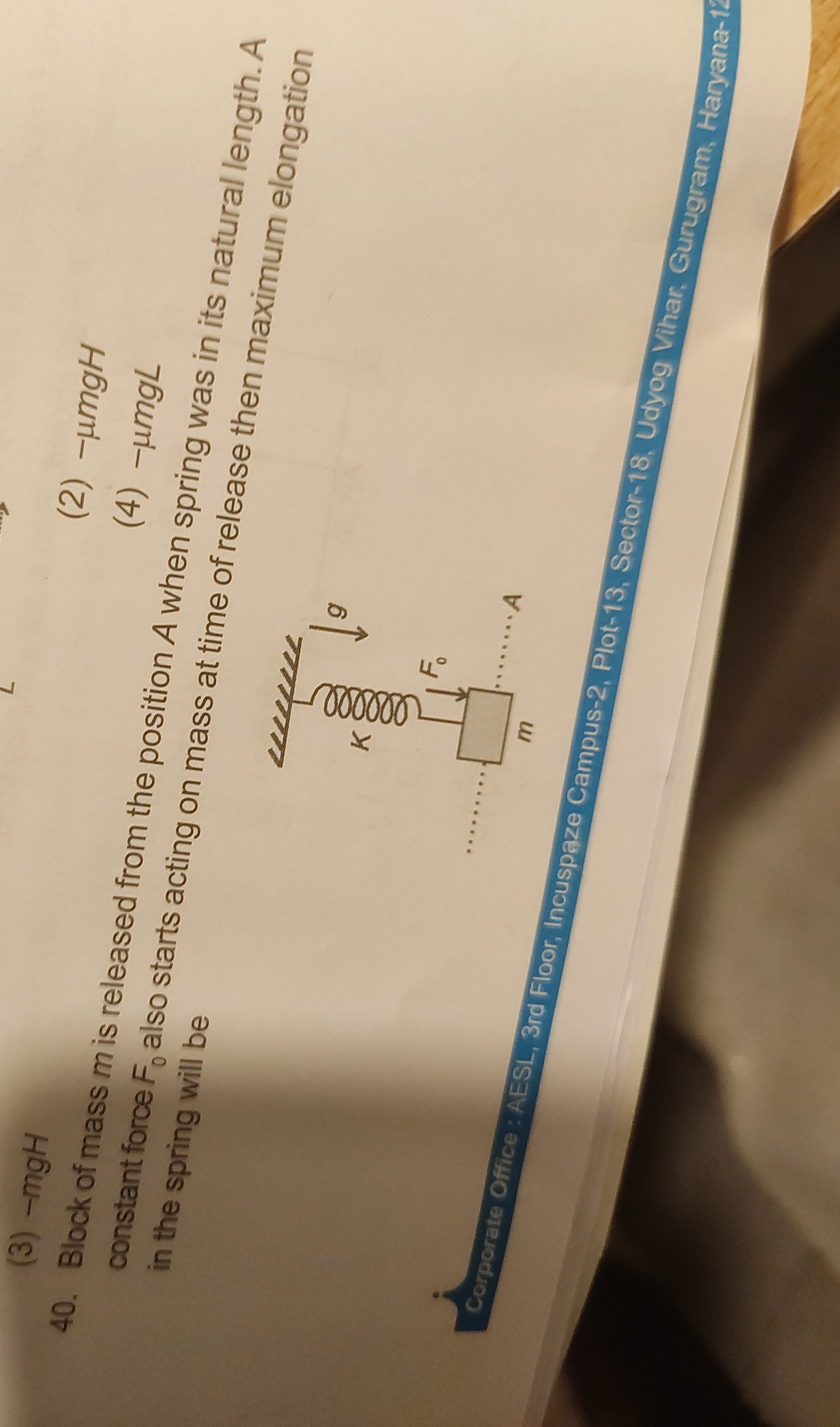
Question: Block of mass m is released from the position A when spring was in its natural length. A constant fo...
Block of mass m is released from the position A when spring was in its natural length. A constant force Fo also starts acting on mass at time of release then maximum elongation in the spring will be
K2(mg+Fo)
Solution
The problem asks for the maximum elongation in a spring when a block of mass 'm' is released from rest. Initially, the spring is at its natural length. A constant force Fo also acts on the mass downwards.
1. Identify the initial and final states:
-
Initial state (A): The block is at rest (vi=0). The spring is at its natural length (spring potential energy Us,i=0). Let's set the gravitational potential energy reference at position A (Ug,i=0).
-
Final state (B): The block reaches its maximum elongation, meaning it momentarily comes to rest (vf=0). Let the maximum elongation be 'x'.
2. Apply the Work-Energy Theorem:
The Work-Energy Theorem states that the net work done on an object equals the change in its kinetic energy: Wnet=ΔKE=KEf−KEi
Since the block starts from rest and momentarily stops at maximum elongation, both initial and final kinetic energies are zero: KEi=0 KEf=0 Therefore, ΔKE=0. So, Wnet=0.
3. Calculate the work done by each force:
The forces acting on the block are:
-
Gravity (mg): Acts downwards. As the block moves downwards by a distance 'x', the work done by gravity is Wg=mgx.
-
Constant force (Fo): Acts downwards. As the block moves downwards by a distance 'x', the work done by Fo is WFo=Fox.
-
Spring force (kx): Acts upwards (opposite to the displacement) as the spring elongates downwards. The spring force is a variable force. The work done by the spring force is Ws=−21kx2.
4. Set up the Work-Energy equation:
Sum of work done by all forces equals zero: Wg+WFo+Ws=0 mgx+Fox−21kx2=0
5. Solve for the maximum elongation (x):
Factor out 'x' from the equation: x(mg+Fo−21kx)=0
This equation gives two possible solutions:
-
x=0: This corresponds to the initial position where the spring is at its natural length.
-
mg+Fo−21kx=0: This corresponds to the position of maximum elongation.
From the second solution: 21kx=mg+Fo x=K2(mg+Fo)
This is the maximum elongation in the spring.
The options provided in the question (e.g., -μmgH, -mgH, -μmgL) are expressions for work or energy, not for elongation. They seem to belong to a different question. Therefore, the answer is the derived expression for maximum elongation.
The final answer is K2(mg+Fo)
