Question

$(1+x^2)(\frac{dy}{dx})+y=e^{\tan^{-1}x}$

Answer 1

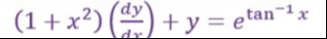
The solution to the differential equation is:

$y = \frac{1}{2}e^{\tan^{-1}x} + C e^{-\tan^{-1}x}$

Answer 2

The given differential equation is a first-order linear differential equation.

1. Rewrite the equation in the standard form $\frac{dy}{dx} + P(x)y = Q(x)$ by dividing by $(1+x^2)$.

2. Identify $P(x) = \frac{1}{1+x^2}$ and $Q(x) = \frac{e^{\tan^{-1}x}}{1+x^2}$.

3. Calculate the integrating factor $IF = e^{\int P(x) dx} = e^{\int \frac{1}{1+x^2} dx} = e^{\tan^{-1}x}$.

4. Apply the general solution formula $y \cdot (IF) = \int Q(x) \cdot (IF) dx + C$.

5. Substitute the expressions for $Q(x)$ and $IF$ into the formula: $y \cdot e^{\tan^{-1}x} = \int \frac{e^{\tan^{-1}x}}{1+x^2} \cdot e^{\tan^{-1}x} dx + C$.

6. Simplify the integral to $\int \frac{(e^{\tan^{-1}x})^2}{1+x^2} dx$.

7. Use substitution $u = \tan^{-1}x$, so $du = \frac{1}{1+x^2} dx$. The integral becomes $\int e^{2u} du = \frac{1}{2}e^{2u}$.

8. Substitute back $u = \tan^{-1}x$ to get $\frac{1}{2}e^{2\tan^{-1}x}$.

9. Equate $y \cdot e^{\tan^{-1}x} = \frac{1}{2}e^{2\tan^{-1}x} + C$.

10. Solve for $y$ by dividing by $e^{\tan^{-1}x}$, yielding $y = \frac{1}{2}e^{\tan^{-1}x} + C e^{-\tan^{-1}x}$.