Question

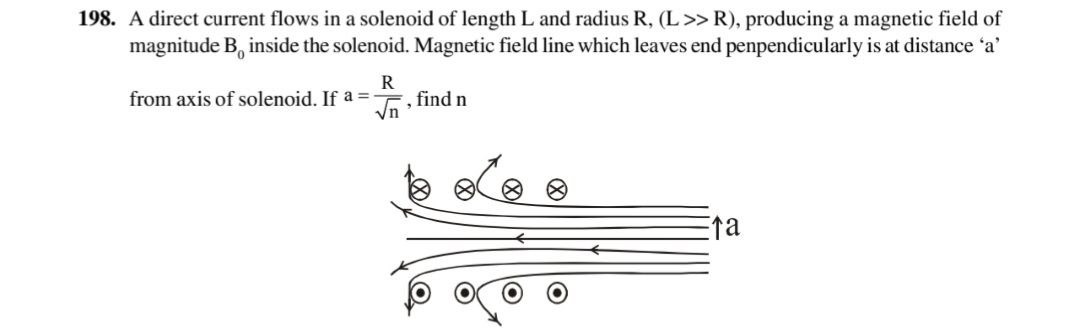
A direct current flows in a solenoid of length L and radius R, (L >> R), producing a magnetic field of magnitude $B_0$ inside the solenoid. Magnetic field line which leaves end penpendicularly is at distance 'a' from axis of solenoid. If a = $\frac{R}{\sqrt{n}}$, find n

Answer 1

2

Answer 2

For a long solenoid of length $L$ and radius $R$ with $L \gg R$, carrying a current $I$, the magnetic field inside is approximately uniform and parallel to the axis, with magnitude $B_0 = \mu_0 n_t I$, where $n_t$ is the number of turns per unit length. The magnetic field outside is very weak except near the ends.

The problem states that a magnetic field line leaves the end perpendicularly at a distance 'a' from the axis. This means that at a point on the end face at a radial distance 'a' from the axis, the magnetic field vector is parallel to the axis. Let the axis of the solenoid be along the x-axis, and let the end face be at $x = L/2$. In cylindrical coordinates $(r, \phi, x)$, the magnetic field at a point $(r, \phi, L/2)$ is $\mathbf{B}(r, \phi, L/2) = B_r(r, \phi, L/2) \hat{\mathbf{r}} + B_\phi(r, \phi, L/2) \hat{\phi} + B_x(r, \phi, L/2) \hat{\mathbf{x}}$. Due to symmetry, $B_\phi = 0$ and $B_r$ and $B_x$ are independent of $\phi$. So, $\mathbf{B}(r, L/2) = B_r(r, L/2) \hat{\mathbf{r}} + B_x(r, L/2) \hat{\mathbf{x}}$.

The condition that a magnetic field line leaves the end perpendicularly at distance 'a' from the axis means that at $r=a$ on the end face, the magnetic field is purely axial, i.e., $B_r(a, L/2) = 0$.

For a long solenoid, it is known that the magnetic field line that leaves the end perpendicularly is at a distance $a = R/\sqrt{2}$ from the axis. This result comes from calculating the magnetic field components at the end face. At this radius, the radial component of the magnetic field is zero.

Given $a = \frac{R}{\sqrt{n}}$, and $a = \frac{R}{\sqrt{2}}$, we have $\frac{R}{\sqrt{n}} = \frac{R}{\sqrt{2}}$. Squaring both sides, $\frac{1}{n} = \frac{1}{2}$, so $n = 2$.