Question
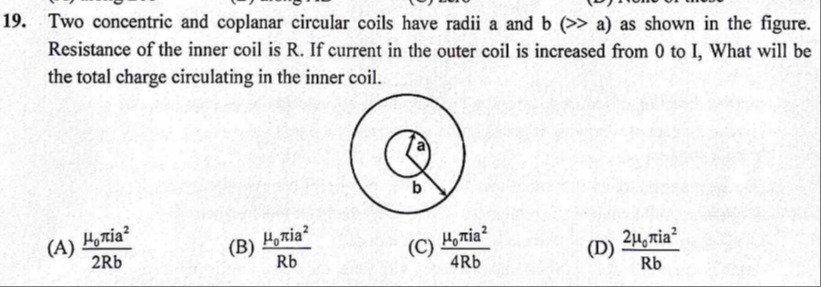
Question: Two concentric and coplanar circular coils have radii a and b (>> a) as shown in the figure. Resista...
Two concentric and coplanar circular coils have radii a and b (>> a) as shown in the figure. Resistance of the inner coil is R. If current in the outer coil is increased from 0 to I, What will be the total charge circulating in the inner coil.
2Rbμ0πia2
Rbμ0πia2
4Rbμ0πia2
Rb2μ0πia2
(A)
Solution
The magnetic field produced by the outer coil at its center is B=2bμ0I. Due to b≫a, this field is approximately uniform over the inner coil's area. The magnetic flux through the inner coil is Φ=B⋅(πa2)=2bμ0πIa2. When the current in the outer coil increases from 0 to I, the change in magnetic flux is ΔΦ=2bμ0πIa2. The total charge (Q) circulating in the inner coil is given by Q=RΔΦ, where R is the resistance of the inner coil. Substituting ΔΦ, we get Q=2Rbμ0πIa2.
