Question
Question: The solution of $2^x + 2^{|x|} \geq 2\sqrt{2}$ is...
The solution of 2x+2∣x∣≥22 is
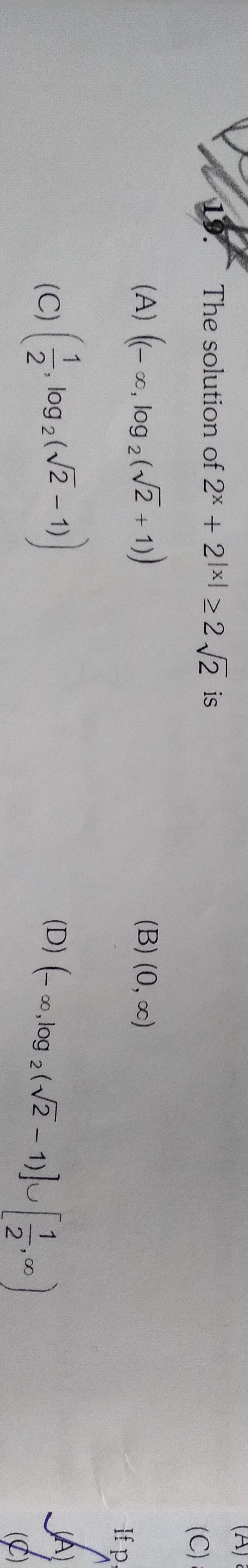
A
(−∞,log2(2+1))
B
(0,∞)
C
(21,log2(2−1))
D
(−∞,log2(2−1)]∪[21,∞)
Answer
(−∞,log2(2−1)]∪[21,∞)
Explanation
Solution
- Case x≥0: ∣x∣=x⟹2x+2x≥22⟹2⋅2x≥22⟹2x+1≥23/2⟹x+1≥3/2⟹x≥1/2. Solution: [1/2,∞).
- Case x<0: ∣x∣=−x⟹2x+2−x≥22. Let y=2x, so 0<y<1. Inequality becomes y+1/y≥22⟹y2−22y+1≥0. Roots are 2±1. So y≤2−1 or y≥2+1. With 0<y<1, we get 0<y≤2−1. Thus 0<2x≤2−1⟹x≤log2(2−1). Solution: (−∞,log2(2−1)].
- Union of solutions: (−∞,log2(2−1)]∪[1/2,∞).
