Question
Question: The solution of $2^x + 2^{|x|} \ge 2\sqrt{2}$ is...
The solution of 2x+2∣x∣≥22 is
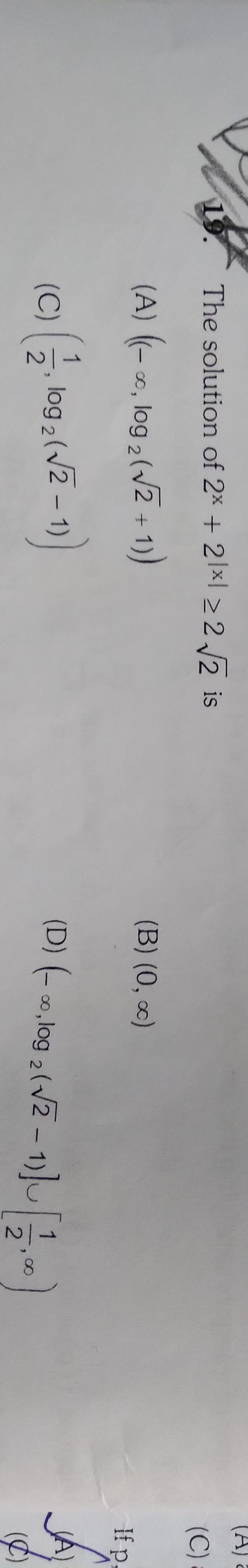
(−∞,log2(2+1))
(0,∞)
(21,log2(2−1))
(−∞,log2(2−1)]∪[21,∞)
(−∞,log2(2−1)]∪[21,∞)
Solution
We need to solve the inequality 2x+2∣x∣≥22. We consider two cases for ∣x∣:
Case 1: x≥0 If x≥0, then ∣x∣=x. The inequality becomes: 2x+2x≥22 2⋅2x≥22 2x+1≥21⋅21/2 2x+1≥23/2 Since the base 2>1, we can compare the exponents: x+1≥23 x≥23−1 x≥21 The solution for this case, considering x≥0, is x∈[21,∞).
Case 2: x<0 If x<0, then ∣x∣=−x. The inequality becomes: 2x+2−x≥22 Let y=2x. Since x<0, we have 0<y<1. The inequality in terms of y is: y+y1≥22 Multiply by y (which is positive, so the inequality direction is preserved): y2+1≥22y Rearrange into a quadratic inequality: y2−22y+1≥0 To find the roots of y2−22y+1=0, we use the quadratic formula: y=222±(−22)2−4(1)(1)=222±8−4=222±4=222±2=2±1. The roots are y1=2−1 and y2=2+1. Since the quadratic has a positive leading coefficient, y2−22y+1≥0 when y≤2−1 or y≥2+1.
Now we apply the condition 0<y<1:
- y≤2−1: Since 2−1≈0.414, this condition is compatible with 0<y<1. Substituting back y=2x: 2x≤2−1. Taking log2 on both sides: x≤log2(2−1). This is consistent with x<0 as log2(2−1)<0. The solution from this part is (−∞,log2(2−1)].
- y≥2+1: Since 2+1≈2.414, this condition (y≥2.414) contradicts 0<y<1. Thus, there is no solution from this part for x<0.
Combining the cases: The total solution set is the union of the solutions from Case 1 and Case 2: (−∞,log2(2−1)]∪[21,∞).
