Question

The set S, is defined as $S = \{(p,q, r) \in N^3: LCM(p, q, r) = 2^53^64^85^9 \text{ and }HCF(p, q, r) = 2^23^34^45^5 \}$.

Then, the digit in units place of n(S), is equal to

Answer 1

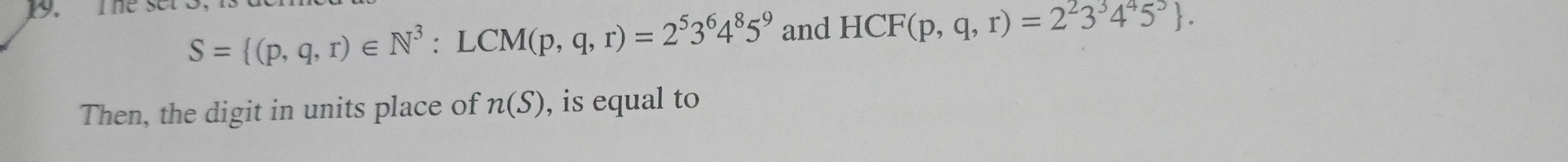
2

Answer 2

Let $p, q, r$ be three natural numbers. We are given their HCF and LCM.

Let the prime factorization of $p, q, r$ be: $p = 2^{a_1}3^{b_1}5^{c_1} \dots$ $q = 2^{a_2}3^{b_2}5^{c_2} \dots$ $r = 2^{a_3}3^{b_3}5^{c_3} \dots$ where $a_i, b_i, c_i, \dots$ are non-negative integers.

The HCF of $p, q, r$ is given by $H = 2^23^34^45^5 = 2^23^3(2^2)^45^5 = 2^23^32^85^5 = 2^{10}3^35^5$. The LCM of $p, q, r$ is given by $L = 2^53^64^85^9 = 2^53^6(2^2)^85^9 = 2^53^62^{16}5^9 = 2^{21}3^65^9$.

For each prime factor, the minimum of the exponents in $p, q, r$ must equal the exponent in the HCF, and the maximum of the exponents must equal the exponent in the LCM.

For the prime factor 2, let the exponents be $a_1, a_2, a_3$. $\min(a_1, a_2, a_3) = 10$ $\max(a_1, a_2, a_3) = 21$ where $a_1, a_2, a_3$ are non-negative integers. Since $\min(a_1, a_2, a_3) = 10$ and $\max(a_1, a_2, a_3) = 21$, we must have $10 \le a_i \le 21$ for $i=1, 2, 3$. Let $N_2$ be the number of such triples $(a_1, a_2, a_3)$. The set of possible values for $a_i$ is $\{10, 11, \dots, 21\}$, which has $21 - 10 + 1 = 12$ elements. The total number of triples $(a_1, a_2, a_3)$ with $10 \le a_i \le 21$ is $12^3$. We need to subtract the triples where $\min(a_1, a_2, a_3) > 10$ or $\max(a_1, a_2, a_3) < 21$. $\min(a_1, a_2, a_3) > 10$ means $a_i > 10$ for all $i$, i.e., $11 \le a_i \le 21$. The number of such triples is $11^3$. $\max(a_1, a_2, a_3) < 21$ means $a_i < 21$ for all $i$, i.e., $10 \le a_i \le 20$. The number of such triples is $11^3$. $\min(a_1, a_2, a_3) > 10$ and $\max(a_1, a_2, a_3) < 21$ means $11 \le a_i \le 20$ for all $i$. The number of such triples is $10^3$. By the Principle of Inclusion-Exclusion, the number of triples where $\min(a_1, a_2, a_3) > 10$ or $\max(a_1, a_2, a_3) < 21$ is $11^3 + 11^3 - 10^3 = 2 \cdot 11^3 - 10^3$. The number of triples satisfying $\min(a_1, a_2, a_3) = 10$ and $\max(a_1, a_2, a_3) = 21$ is $N_2 = 12^3 - (2 \cdot 11^3 - 10^3) = 12^3 - 2 \cdot 11^3 + 10^3$. $N_2 = 1728 - 2 \cdot 1331 + 1000 = 1728 - 2662 + 1000 = 66$.

Alternatively, consider the values $a_1, a_2, a_3$. They must be chosen from $\{10, 11, \dots, 21\}$. The set of values $\{a_1, a_2, a_3\}$ must contain 10 and 21. Case 1: $\{a_1, a_2, a_3\} = \{10, 21, k\}$ where $10 < k < 21$. There are $20 - 11 + 1 = 10$ possible values for $k$. For each $k$, the triple $(10, 21, k)$ and its permutations are possible. The values 10, 21, $k$ are distinct. There are $3! = 6$ permutations. Number of triples = $10 \times 6 = 60$. Case 2: $\{a_1, a_2, a_3\} = \{10, 10, 21\}$. The possible triples are permutations of $(10, 10, 21)$. There are $\frac{3!}{2!} = 3$ permutations: $(10, 10, 21), (10, 21, 10), (21, 10, 10)$. Number of triples = 3. Case 3: $\{a_1, a_2, a_3\} = \{10, 21, 21\}$. The possible triples are permutations of $(10, 21, 21)$. There are $\frac{3!}{2!} = 3$ permutations: $(10, 21, 21), (21, 10, 21), (21, 21, 10)$. Number of triples = 3. Total number of triples $N_2 = 60 + 3 + 3 = 66$.

For the prime factor 3, let the exponents be $b_1, b_2, b_3$. $\min(b_1, b_2, b_3) = 3$ $\max(b_1, b_2, b_3) = 6$ where $b_1, b_2, b_3$ are non-negative integers. The set of possible values for $b_i$ is $\{3, 4, 5, 6\}$, which has $6 - 3 + 1 = 4$ elements. Let $N_3$ be the number of such triples $(b_1, b_2, b_3)$. Using the formula $N = m^3 - 2(m-1)^3 + (m-2)^3$, where $m$ is the number of values in the range $[min, max]$. Here $m = 4$. $N_3 = 4^3 - 2 \cdot 3^3 + 2^3 = 64 - 2 \cdot 27 + 8 = 64 - 54 + 8 = 10 + 8 = 18$.

For the prime factor 5, let the exponents be $c_1, c_2, c_3$. $\min(c_1, c_2, c_3) = 5$ $\max(c_1, c_2, c_3) = 9$ where $c_1, c_2, c_3$ are non-negative integers. The set of possible values for $c_i$ is $\{5, 6, 7, 8, 9\}$, which has $9 - 5 + 1 = 5$ elements. Let $N_5$ be the number of such triples $(c_1, c_2, c_3)$. Using the formula $N = m^3 - 2(m-1)^3 + (m-2)^3$, where $m = 5$. $N_5 = 5^3 - 2 \cdot 4^3 + 3^3 = 125 - 2 \cdot 64 + 27 = 125 - 128 + 27 = -3 + 27 = 24$.

For any other prime factor $k$, let the exponents be $d_1, d_2, d_3$. $\min(d_1, d_2, d_3) = 0$ (from HCF) $\max(d_1, d_2, d_3) = 0$ (from LCM) This implies $d_1 = d_2 = d_3 = 0$. There is only $1$ possibility for the exponents of any other prime.

The total number of triples $(p, q, r)$ is the product of the number of possibilities for the exponents of each prime factor. $n(S) = N_2 \times N_3 \times N_5$. $n(S) = 66 \times 18 \times 24$.

We need to find the digit in the units place of $n(S)$. This is the units digit of $66 \times 18 \times 24$. The units digit of a product is the units digit of the product of the units digits of the factors. Units digit of 66 is 6. Units digit of 18 is 8. Units digit of 24 is 4. Units digit of $n(S)$ = Units digit of $(6 \times 8 \times 4)$. $6 \times 8 = 48$. Units digit is 8. Units digit of $(48 \times 4)$ = Units digit of $(8 \times 4) = 32$. The units digit is 2.

The final answer is $\boxed{2}$.

Explanation of the solution:

1. Determine the prime factorization of the given HCF and LCM.
2. For each prime factor, the exponents in the triple $(p, q, r)$ must satisfy the minimum and maximum conditions given by the HCF and LCM exponents.
3. For a prime factor with HCF exponent $h$ and LCM exponent $l$, the exponents $(e_1, e_2, e_3)$ in $(p, q, r)$ must satisfy $h \le e_i \le l$ for $i=1, 2, 3$, $\min(e_1, e_2, e_3) = h$, and $\max(e_1, e_2, e_3) = l$.
4. The number of such triples $(e_1, e_2, e_3)$ for a given prime is the number of ways to choose three numbers from the set $\{h, h+1, \dots, l\}$ such that the minimum is $h$ and the maximum is $l$. Let $m = l - h + 1$ be the number of values in the range. The number of such triples is $m^3 - 2(m-1)^3 + (m-2)^3$.
5. Calculate the number of possibilities for the exponents of each prime factor (2, 3, and 5).
   • For prime 2: $h=10, l=21$, $m=12$. Number of triples $N_2 = 12^3 - 2(11)^3 + (10)^3 = 1728 - 2(1331) + 1000 = 1728 - 2662 + 1000 = 66$.
   • For prime 3: $h=3, l=6$, $m=4$. Number of triples $N_3 = 4^3 - 2(3)^3 + (2)^3 = 64 - 2(27) + 8 = 64 - 54 + 8 = 18$.
   • For prime 5: $h=5, l=9$, $m=5$. Number of triples $N_5 = 5^3 - 2(4)^3 + (3)^3 = 125 - 2(64) + 27 = 125 - 128 + 27 = 24$.
6. The total number of elements in set S is the product of the number of possibilities for each prime factor's exponents: $n(S) = N_2 \times N_3 \times N_5 = 66 \times 18 \times 24$.
7. To find the units digit of $n(S)$, multiply the units digits of the factors: Units digit of $(6 \times 8 \times 4) =$ Units digit of $(48 \times 4) =$ Units digit of $(8 \times 4) =$ Units digit of $(32) = 2$.