Question

Prove that the equation to the circle of which the points $(x_1,y_1)$ and $(x_2,y_2)$ are the ends of a chord of a segment containing an angle $\theta$ is $(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = \pm \cot \theta [(x-x_1)(y-y_2) - (x-x_2)(y-y_1)] = 0$.

Answer 1

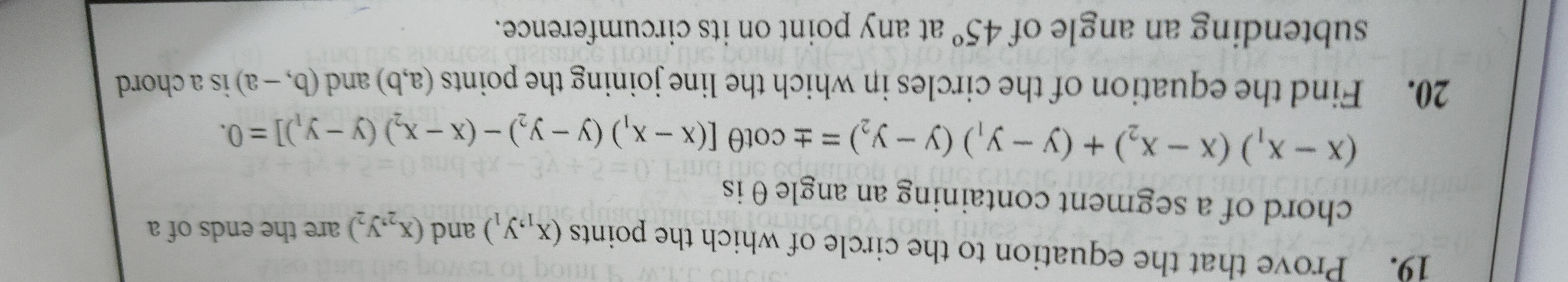
The equation of the circle is $(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = \pm \cot \theta [(x-x_1)(y-y_2) - (x-x_2)(y-y_1)]$.

Answer 2

Let $P(x, y)$ be any point on the circumference of the circle, and let $A = (x_1, y_1)$ and $B = (x_2, y_2)$ be the endpoints of the chord. The angle subtended by the chord $AB$ at point $P$ is $\angle APB = \theta$. The slope of $PA$ is $m_{PA} = \frac{y - y_1}{x - x_1}$ and the slope of $PB$ is $m_{PB} = \frac{y - y_2}{x - x_2}$. Using the formula for the angle between two lines, $\tan \theta = \left| \frac{m_{PA} - m_{PB}}{1 + m_{PA} m_{PB}} \right|$, and simplifying, we get $\tan \theta = \left| \frac{(y - y_1)(x - x_2) - (y - y_2)(x - x_1)}{(x - x_1)(x - x_2) + (y - y_1)(y - y_2)} \right|$. Let $S = (x - x_1)(x - x_2) + (y - y_1)(y - y_2)$ and $N = (y - y_1)(x - x_2) - (y - y_2)(x - x_1)$. Then $\tan \theta = \left| \frac{N}{S} \right|$, which implies $S \tan \theta = \pm N$. Substituting back the expressions for $S$ and $N$, we get $[(x - x_1)(x - x_2) + (y - y_1)(y - y_2)] \tan \theta = \pm [(y - y_1)(x - x_2) - (y - y_2)(x - x_1)]$. Multiplying by $\cot \theta$, we obtain $(x - x_1)(x - x_2) + (y - y_1)(y - y_2) = \pm \cot \theta [(y - y_1)(x - x_2) - (y - y_2)(x - x_1)]$. The term $(x-x_1)(y-y_2) - (x-x_2)(y-y_1)$ is related to the signed area. The equation can be written as $(x-x_1)(x-x_2) + (y-y_1)(y-y_2) = \pm \cot \theta [(x-x_1)(y-y_2) - (x-x_2)(y-y_1)]$. The $\pm$ sign accounts for the two possible segments where the angle $\theta$ can be subtended.