Question

Let $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ be three non-coplanar vectors and $\overrightarrow{r}$ be any arbitrary vector, then the expression $(\overrightarrow{a} \times \overrightarrow{b}) \times (\overrightarrow{r} \times \overrightarrow{c}) + (\overrightarrow{b} \times \overrightarrow{c}) \times (\overrightarrow{r} \times \overrightarrow{a}) + (\overrightarrow{c} \times \overrightarrow{a}) \times (\overrightarrow{r} \times \overrightarrow{b})$ is always equal to:

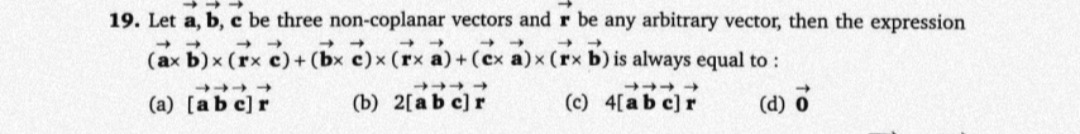
• A. $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r}$
• B. $2[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r}$
• C. $4[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r}$
• D. $\overrightarrow{0}$

Answer 1

Answer: (B)

2[a b c]r

Answer 2

The given expression is $E = (\overrightarrow{a} \times \overrightarrow{b}) \times (\overrightarrow{r} \times \overrightarrow{c}) + (\overrightarrow{b} \times \overrightarrow{c}) \times (\overrightarrow{r} \times \overrightarrow{a}) + (\overrightarrow{c} \times \overrightarrow{a}) \times (\overrightarrow{r} \times \overrightarrow{b})$.

Using the vector triple product identity $\overrightarrow{P} \times (\overrightarrow{Q} \times \overrightarrow{R}) = (\overrightarrow{P} \cdot \overrightarrow{R})\overrightarrow{Q} - (\overrightarrow{P} \cdot \overrightarrow{Q})\overrightarrow{R}$:

Term 1: $(\overrightarrow{a} \times \overrightarrow{b}) \times (\overrightarrow{r} \times \overrightarrow{c}) = ((\overrightarrow{a} \times \overrightarrow{b}) \cdot \overrightarrow{c})\overrightarrow{r} - ((\overrightarrow{a} \times \overrightarrow{b}) \cdot \overrightarrow{r})\overrightarrow{c} = [\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} - [\overrightarrow{a}\overrightarrow{b}\overrightarrow{r}]\overrightarrow{c}$.

Term 2: $(\overrightarrow{b} \times \overrightarrow{c}) \times (\overrightarrow{r} \times \overrightarrow{a}) = ((\overrightarrow{b} \times \overrightarrow{c}) \cdot \overrightarrow{a})\overrightarrow{r} - ((\overrightarrow{b} \times \overrightarrow{c}) \cdot \overrightarrow{r})\overrightarrow{a} = [\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} - [\overrightarrow{b}\overrightarrow{c}\overrightarrow{r}]\overrightarrow{a}$.

Term 3: $(\overrightarrow{c} \times \overrightarrow{a}) \times (\overrightarrow{r} \times \overrightarrow{b}) = ((\overrightarrow{c} \times \overrightarrow{a}) \cdot \overrightarrow{b})\overrightarrow{r} - ((\overrightarrow{c} \times \overrightarrow{a}) \cdot \overrightarrow{r})\overrightarrow{b} = [\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} - [\overrightarrow{c}\overrightarrow{a}\overrightarrow{r}]\overrightarrow{b}$.

Adding the three terms: $E = 3[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} - ([\overrightarrow{a}\overrightarrow{b}\overrightarrow{r}]\overrightarrow{c} + [\overrightarrow{b}\overrightarrow{c}\overrightarrow{r}]\overrightarrow{a} + [\overrightarrow{c}\overrightarrow{a}\overrightarrow{r}]\overrightarrow{b})$.

Using the identity $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} = [\overrightarrow{r}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{a} + [\overrightarrow{r}\overrightarrow{c}\overrightarrow{a}]\overrightarrow{b} + [\overrightarrow{r}\overrightarrow{a}\overrightarrow{b}]\overrightarrow{c} = [\overrightarrow{b}\overrightarrow{c}\overrightarrow{r}]\overrightarrow{a} + [\overrightarrow{c}\overrightarrow{a}\overrightarrow{r}]\overrightarrow{b} + [\overrightarrow{a}\overrightarrow{b}\overrightarrow{r}]\overrightarrow{c}$, the term in parenthesis is equal to $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r}$.

Therefore, $E = 3[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} - [\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r} = 2[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]\overrightarrow{r}$.