Question
Question: Let $f(x)=\begin{cases} (x-1)(x-n) & x \leq n \\ x^{2}-n & x > n \end{cases}$, then identify correct...
Let f(x)={(x−1)(x−n)x2−nx≤nx>n, then identify correct statement(s) (n∈I)
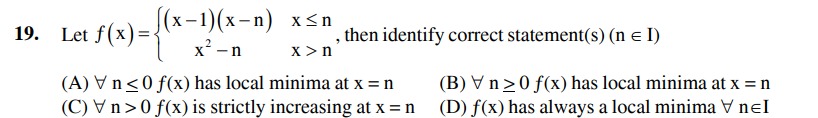
∀ n ≤ 0 f(x) has local minima at x = n
∀ n ≥ 0 f(x) has local minima at x = n
∀ n > 0 f(x) is strictly increasing at x = n
f(x) has always a local minima ∀ n∈I
A
Solution
The function is given by: f(x)={(x−1)(x−n)x2−nx≤nx>n where n∈I (n is an integer).
First, let's evaluate f(x) at x=n: f(n)=(n−1)(n−n)=(n−1)⋅0=0.
For f(x) to have a local minimum at x=n, there must exist an open interval (n−δ,n+δ) such that f(x)≥f(n) for all x∈(n−δ,n+δ). Since f(n)=0, we need f(x)≥0 in this interval.
Let's analyze the two parts of the function around x=n:
-
For x>n (and close to n): f(x)=x2−n. We need x2−n≥0. Let x=n+ϵ for a small ϵ>0. f(n+ϵ)=(n+ϵ)2−n=n2+2nϵ+ϵ2−n=(n2−n)+(2nϵ+ϵ2). We need (n2−n)+(2nϵ+ϵ2)≥0 for small ϵ>0. If n2−n>0, this condition is satisfied for small ϵ. (n(n−1)>0⟹n∈(−∞,0)∪(1,∞)). If n2−n=0, i.e., n=0 or n=1, then f(n+ϵ)=2nϵ+ϵ2. For n=0, f(ϵ)=ϵ2≥0. For n=1, f(1+ϵ)=2ϵ+ϵ2≥0 for small ϵ>0. So, for x>n and close to n, f(x)≥f(n) is always true for any integer n.
-
For x≤n (and close to n): f(x)=(x−1)(x−n). We need (x−1)(x−n)≥0. Let x=n−ϵ for a small ϵ>0. f(n−ϵ)=((n−ϵ)−1)((n−ϵ)−n)=(n−1−ϵ)(−ϵ)=−ϵ(n−1−ϵ). For f(n−ϵ)≥0, we need −ϵ(n−1−ϵ)≥0. Since ϵ>0, we must have −(n−1−ϵ)≥0, which implies n−1−ϵ≤0. So, n−1≤ϵ.
This condition must hold for some sufficiently small ϵ>0.
- If n−1≤0 (i.e., n≤1), then for any small ϵ>0, we can choose ϵ such that n−1≤ϵ. In this case, n−1−ϵ≤0, so −ϵ(n−1−ϵ)≥0. Thus, if n≤1, f(x)≥f(n) for x<n and close to n.
- If n−1>0 (i.e., n>1), then we can choose ϵ such that 0<ϵ<n−1. For such an ϵ, n−1−ϵ>0. In this case, f(n−ϵ)=−ϵ(n−1−ϵ)<0. This means f(x)<f(n) for x slightly less than n. Therefore, if n>1, f(x) does not have a local minimum at x=n.
Combining the results from both sides, f(x) has a local minimum at x=n if and only if n≤1. Since n∈I, this includes n=1,0,−1,−2,….
Now let's evaluate the given options:
(A) ∀ n ≤ 0 f(x) has local minima at x = n. This statement is true. If n≤0, then n is certainly ≤1. So, f(x) has a local minimum at x=n.
(B) ∀ n ≥ 0 f(x) has local minima at x = n. This statement is false. For example, if n=2, then n≥0 but n>1. Our analysis shows that for n>1, f(x) does not have a local minimum at x=n.
(C) ∀ n > 0 f(x) is strictly increasing at x = n. For f(x) to be strictly increasing at x=n, we would need f(x1)<f(x2) for x1<x2 in a neighborhood of n. Consider n=1. We found f(x) has a local minimum at x=1. A function with a local minimum is not strictly increasing at that point. Consider n>1. For x∈(1,n), f(x)=(x−1)(x−n). Since x−1>0 and x−n<0, f(x)<0. Since f(n)=0, we have f(x)<f(n) for x approaching n from the left. This means f(x) is decreasing as x→n−. Therefore, f(x) is not strictly increasing at x=n for n>0. This statement is false.
(D) f(x) has always a local minima ∀ n∈I. This statement is false. As shown, f(x) only has a local minimum at x=n if n≤1. For n>1, it does not.
The only correct statement is (A).
