Question

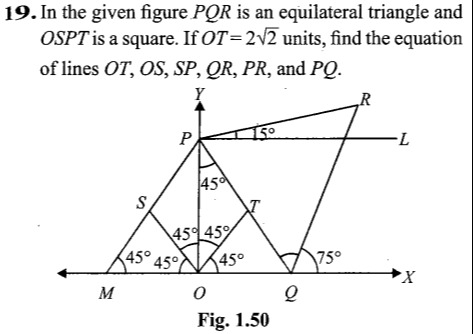
In the given figure $PQR$ is an equilateral triangle and $OSPT$ is a square. If $OT = 2\sqrt{2}$ units, find the equation of lines $OT$, $OS$, $SP$, $QR$, $PR$, and $PQ$.

Answer 1

Line $OT$: $y = x$, Line $OS$: $y = -x$, Line $SP$: $y = x+4$, Line $QR$: $y = (2+\sqrt{3})(x-4)$, Line $PR$: $y = (2-\sqrt{3})x+4$, Line $PQ$: $y = -x+4$

Answer 2

1. Square Vertices: Given $OT = 2\sqrt{2}$ and $OSPT$ is a square with $O$ at the origin.

   • $T = (2\sqrt{2} \cos 45^\circ, 2\sqrt{2} \sin 45^\circ) = (2,2)$.
   • $S = (2\sqrt{2} \cos 135^\circ, 2\sqrt{2} \sin 135^\circ) = (-2,2)$.
   • $P = S + T = (-2,2) + (2,2) = (0,4)$.

2. Square Lines:

   • $OT$: Passes through $(0,0)$ and $(2,2)$. Equation: $y=x$.
   • $OS$: Passes through $(0,0)$ and $(-2,2)$. Equation: $y=-x$.
   • $SP$: Passes through $S(-2,2)$ and $P(0,4)$. Slope $m_{SP} = \frac{4-2}{0-(-2)} = 1$. Equation: $y-4 = 1(x-0) \Rightarrow y=x+4$.

3. Equilateral Triangle Lines: $P=(0,4)$.

   • $PQR$ is equilateral. From the figure, the line $PR$ makes an angle of $15^\circ$ with the $X$-axis.
   • Slope of $PR$: $m_{PR} = \tan 15^\circ = 2-\sqrt{3}$.
   • Equation of $PR$: $y-4 = (2-\sqrt{3})x \Rightarrow y = (2-\sqrt{3})x+4$.
   • The angle of $PQ$ with $X$-axis is $15^\circ - 60^\circ = -45^\circ$.
   • Slope of $PQ$: $m_{PQ} = \tan (-45^\circ) = -1$.
   • Equation of $PQ$: $y-4 = -1x \Rightarrow y = -x+4$.
   • If $Q$ is on the $X$-axis ($y_Q=0$), then $0=-x_Q+4 \Rightarrow x_Q=4$. So $Q=(4,0)$.
   • The angle of $QR$ with the $X$-axis is $75^\circ$.
   • Slope of $QR$: $m_{QR} = \tan 75^\circ = 2+\sqrt{3}$.
   • Equation of $QR$: $y-0 = (2+\sqrt{3})(x-4) \Rightarrow y = (2+\sqrt{3})(x-4)$.

The equations of the lines are:

• Line $OT$: $y = x$
• Line $OS$: $y = -x$
• Line $SP$: $y = x+4$
• Line $QR$: $y = (2+\sqrt{3})(x-4)$
• Line $PR$: $y = (2-\sqrt{3})x+4$
• Line $PQ$: $y = -x+4$