Question
Question: In the figure, potential difference between A and B is:...
In the figure, potential difference between A and B is:
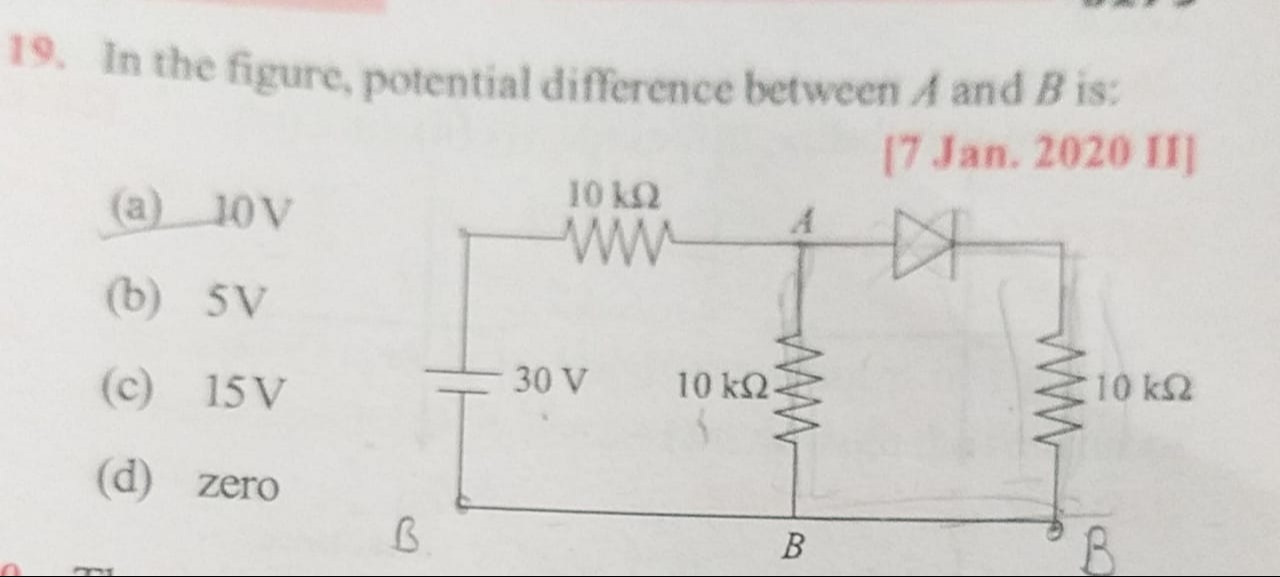
10 V
5 V
15 V
zero
10 V
Solution
Set the potential at point B to 0 V (VB=0). The voltage source is 30 V, so the potential at its positive terminal is 30 V. Let's denote the node before R1 as P, so VP=30 V. Applying KCL at node A: Current through R1 (IR1) + Current through diode (ID) = Current through R2 (IR2) R1VP−VA+ID=R2VA−VB 10 kΩ30−VA+ID=10 kΩVA−0 For an ideal diode, if it conducts, VA=VD and ID>0. If it doesn't conduct, ID=0 and VA<VD. Assume the diode conducts: VA=VD. The current through R3 is IR3=R3VD−VB=10 kΩVA−0. Since ID=IR3 (KCL at D), ID=10 kΩVA. Substituting into the KCL at A: 10 kΩ30−VA+10 kΩVA=10 kΩVA 30−VA+VA=VA 30=2VA⟹VA=15 V If VA=15 V, then VD=15 V. ID=10 kΩ15 V=1.5 mA. Check KCL at A: IR1=1030−15=1.5 mA. IR2=1015−0=1.5 mA. 1.5 mA+1.5 mA=1.5 mA. This assumption is incorrect.
Let's re-evaluate the circuit diagram. The voltage source is connected such that its positive terminal is at the top, and the negative terminal is at B. So, Vsource=Vtop−Vbottom=30 V. If VB=0, then Vbottom=0. This means Vtop=30 V. The node before R1 is Vtop, so VP=30 V. KCL at node A: R1VP−VA=R2VA−VB+Idiode 10 kΩ30−VA=10 kΩVA−0+Idiode Assume diode conducts (VA=VD): Idiode=R3VD−VB=10 kΩVA−0. 10 kΩ30−VA=10 kΩVA+10 kΩVA 30−VA=VA+VA 30=3VA⟹VA=10 V If VA=10 V, then VD=10 V. Idiode=10 kΩ10 V=1 mA. This is >0, so the diode conducts. IR1=1030−10=2 mA. IR2=1010−0=1 mA. KCL at A: IR1=IR2+Idiode⟹2 mA=1 mA+1 mA. This is consistent. Therefore, VA=10 V. The potential difference between A and B is VAB=VA−VB=10 V−0 V=10 V.
