Question

If the vectors $a = 2i + pj + 4k$ and $b = 6i - 9j + qk$ are collinear then p and q are

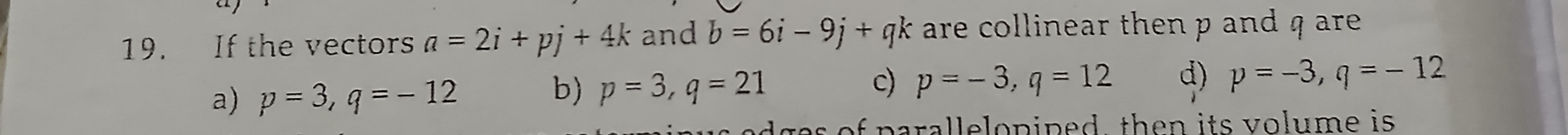
• A. $p = 3, q = -12$
• B. $p = 3, q = 21$
• C. $p = -3, q = 12$
• D. $p = -3, q = -12$

Answer 1

Answer: (C)

Option (c) $p = -3, q = 12$.

Answer 2

Vectors a and b are collinear, so there exists a scalar $\lambda$ such that:

$6i - 9j + qk = \lambda(2i + pj + 4k)$

Comparing the components:

• $i$-component: $6 = 2\lambda \implies \lambda = 3$.
• $j$-component: $-9 = \lambda p \implies -9 = 3p \implies p = -3$.
• $k$-component: $q = 4\lambda \implies q = 4 \times 3 = 12$.