Question

If the lines $\frac{x-1}{2} = \frac{y+1}{3} = \frac{z-1}{4}$ and $\frac{x-2}{1} = \frac{y+m}{2} = \frac{z-2}{1}$ intersect each other, then of $m$ is

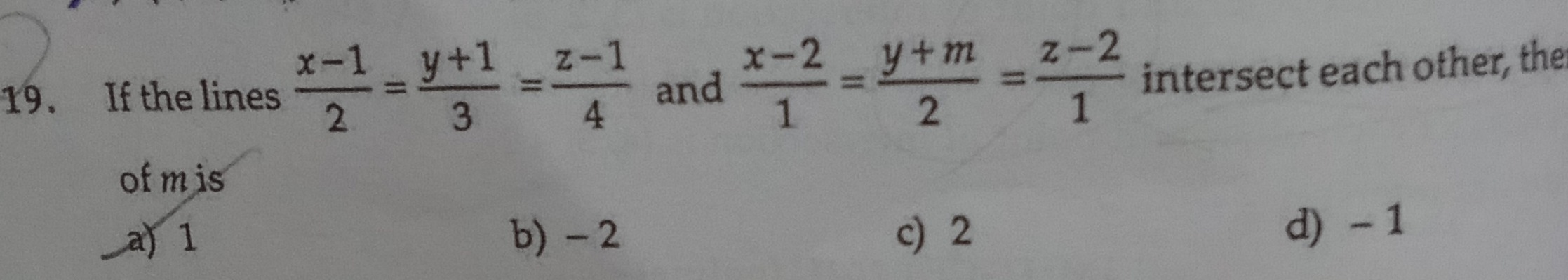
• A. 1
• B. -2
• C. 2
• D.
  • 1

Answer 1

Answer: (D)

m = -1

Answer 2

Let parameter $t$ for the first line:

$$x=1+2t,\quad y=-1+3t,\quad z=1+4t.$$

Let parameter $s$ for the second line:

$$x=2+s,\quad y=2s-m,\quad z=2+s.$$

For the lines to intersect, equate corresponding coordinates.

1. From $x$-coordinates:

   $$1+2t=2+s \implies s=2t-1.$$

2. From $z$-coordinates:

   $$1+4t=2+s \implies 1+4t=2+(2t-1) \implies 1+4t=2t+1.$$

   This gives $4t=2t$ and hence $t=0$.

3. Substitute $t=0$ into $s=2t-1$:

   $$s=-1.$$

4. Equate $y$-coordinates:

   $$-1+3(0)=2(-1)-m \implies -1=-2-m \implies m=-1+2= -1.$$