Question
Question: An open hemisphere is centred at origin. Point A and B are on the y-axis at equal distances from the...
An open hemisphere is centred at origin. Point A and B are on the y-axis at equal distances from the origin. When a point charge q is kept at B, flux from the hemi sphere is ϕ. If the point charge is shifted at A then flux from the hemi sphere will be :-
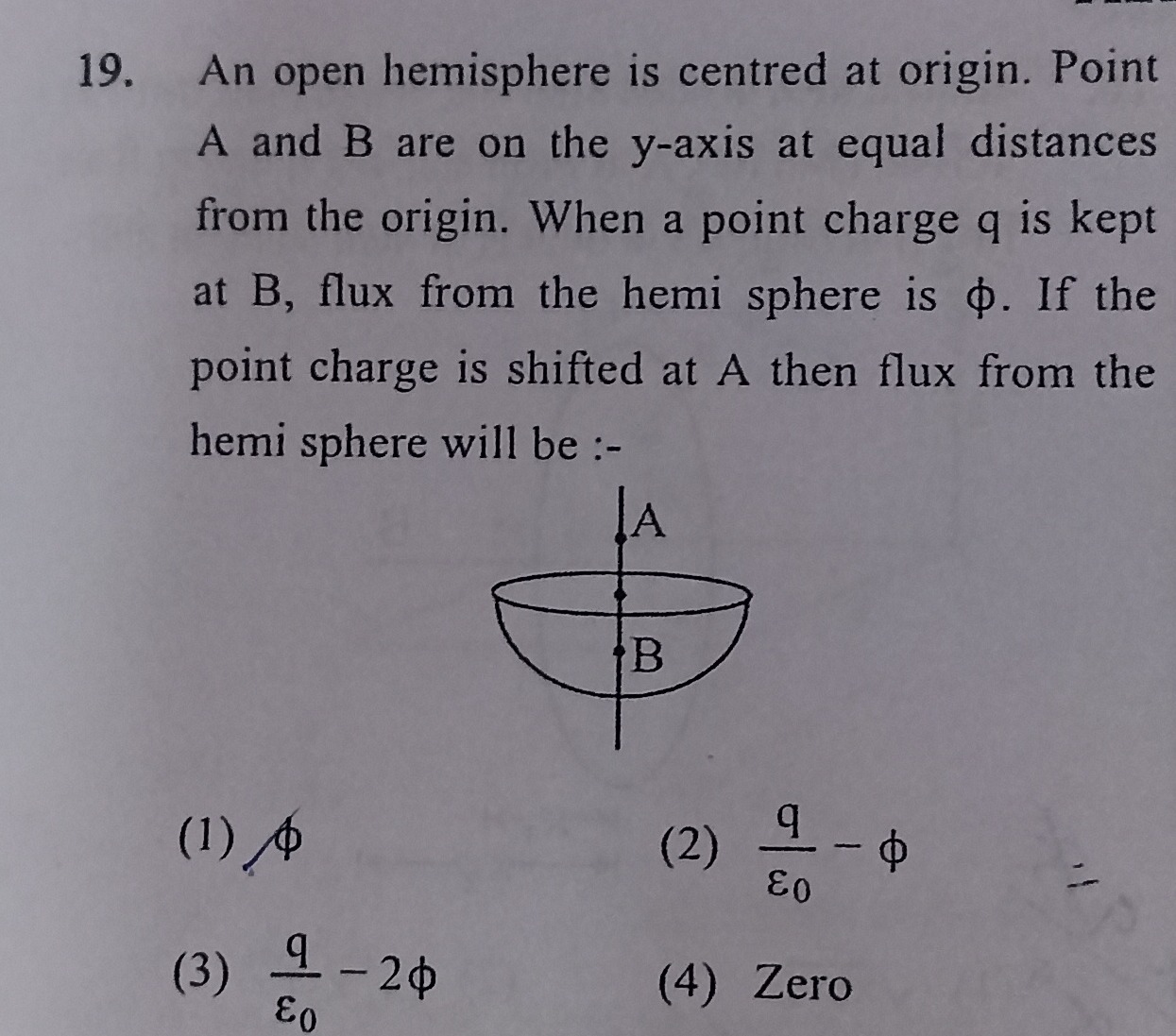
ϕ
ϵ0q−ϕ
ϵ0q−2ϕ
Zero
(2) ϵ0q−ϕ
Solution
To solve this problem, we will use Gauss's Law and the principle of symmetry.
Let the open hemisphere be denoted by Scurved and its flat circular base be denoted by Sbase. Together, Scurved and Sbase form a closed spherical surface Sclosed. The origin is the center of this hemisphere. Points A and B are on the y-axis at equal distances from the origin, meaning they are symmetric with respect to the plane of the base (xy-plane).
Case 1: Point charge q is kept at B.
Let the coordinates of B be (0,−y0), and the origin be (0,0). The hemisphere is centered at the origin, and from the diagram, it's the upper hemisphere (i.e., its curved surface is in the region y>0). Therefore, point B is outside the closed surface formed by the hemisphere and its base.
According to Gauss's Law, the total electric flux through a closed surface enclosing no charge is zero.
So, Φclosed=ΦScurved+ΦSbase=0.
We are given that the flux from the hemisphere (meaning the curved surface) is ϕ.
So, ΦScurved=ϕ.
Substituting this into the Gauss's Law equation:
ϕ+ΦSbase=0
ΦSbase=−ϕ
Here, ΦSbase is the flux through the flat circular base due to the charge q at B. For a closed surface, the area vector for the base points outwards, which is downwards (in the negative y-direction). Since the charge q at B is below the base, the electric field lines from B generally point upwards. Thus, the dot product E⋅dSbase will be negative, meaning ΦSbase is negative. This is consistent with ΦSbase=−ϕ, implying ϕ is a positive value.
Case 2: Point charge q is shifted to A.
Let the coordinates of A be (0,y0). From the diagram, point A is inside the closed surface formed by the hemisphere and its base.
According to Gauss's Law, the total electric flux through a closed surface enclosing a charge q is ϵ0q.
Let the new flux through the curved surface be ϕ′.
Let the new flux through the base be ΦSbase′.
So, Φclosed′=ϕ′+ΦSbase′=ϵ0q.
Now, we need to determine ΦSbase′. This is the flux through the flat circular base due to the charge q at A.
Since A is above the base and B is below the base, and they are equidistant from the origin (symmetric with respect to the base plane), the magnitude of the flux through the base will be the same whether the charge is at A or at B.
∣ΦSbase′∣=∣ΦSbase∣.
From Case 1, we found ΦSbase=−ϕ, so ∣ΦSbase∣=ϕ.
Therefore, ∣ΦSbase′∣=ϕ.
Now, let's consider the sign of ΦSbase′. The charge q at A is above the base, so the electric field lines from A generally point downwards. The area vector for the base (for the closed surface) also points downwards. Since E and dSbase are generally in the same direction, their dot product E⋅dSbase will be positive.
Thus, ΦSbase′ is positive.
Combining the magnitude and sign, we get ΦSbase′=ϕ.
Substitute this value into the Gauss's Law equation for Case 2:
ϕ′+ϕ=ϵ0q
ϕ′=ϵ0q−ϕ
The flux from the hemisphere (curved surface) when the charge is at A will be ϵ0q−ϕ.
The final answer is (2).
Explanation of the solution:
- Form a closed surface: Imagine closing the open hemisphere with a flat circular base. This forms a closed Gaussian surface.
- Apply Gauss's Law (Initial case): When charge q is at B (outside the closed surface), the total flux through the closed surface is zero.
- Flux through curved surface (ϕ) + Flux through base (Φbase) = 0.
- This gives Φbase=−ϕ.
- Apply Gauss's Law (Final case): When charge q is at A (inside the closed surface), the total flux through the closed surface is q/ϵ0.
- New flux through curved surface (ϕ′) + New flux through base (Φbase′) = q/ϵ0.
- Symmetry argument for base flux: Points A and B are equidistant from the origin and symmetric with respect to the base plane. The magnitude of flux through the base is the same for charges at A or B. However, the direction of field lines relative to the outward normal of the base is opposite. From B, field lines go up (normal down, so negative flux). From A, field lines go down (normal down, so positive flux). Therefore, Φbase′=∣Φbase∣=ϕ.
- Calculate new curved surface flux: Substitute Φbase′=ϕ into the Gauss's Law equation for the final case:
- ϕ′+ϕ=q/ϵ0
- ϕ′=q/ϵ0−ϕ.
