Question

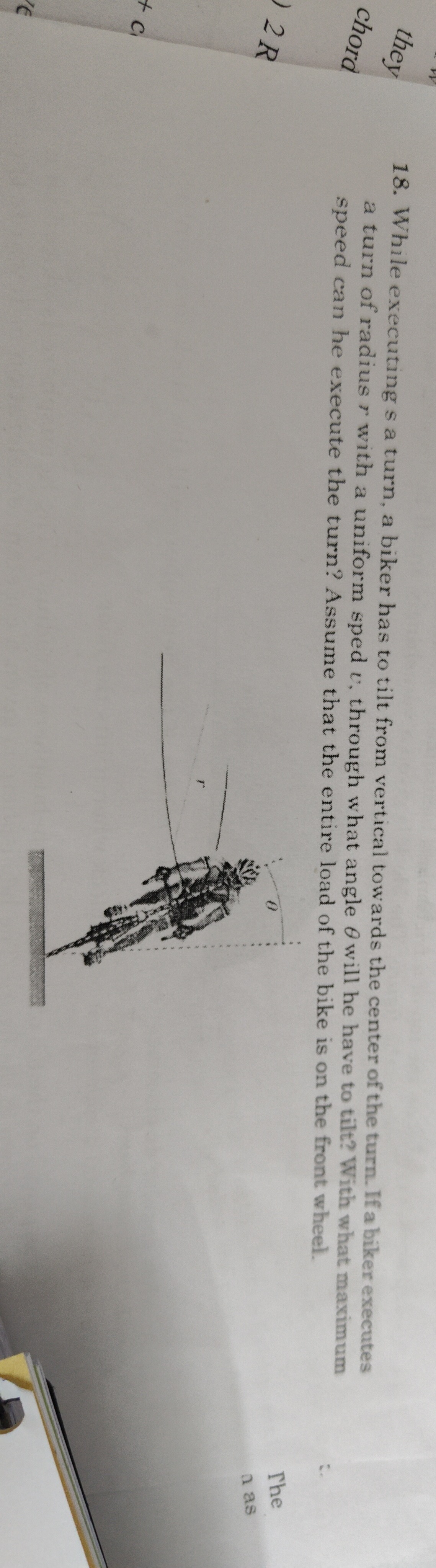
While executing s a turn, a biker has to tilt from vertical towards the center of the turn. If a biker executes a turn of radius r with a uniform sped u, through what angle $\theta$ will he have to tilt? With what maximum speed can he execute the turn? Assume that the entire load of the bike is on the front wheel.

Answer 1

$\theta = \tan^{-1}\left(\frac{u^2}{rg}\right), u_{max} = \sqrt{\mu_s rg}$

Answer 2

To determine the angle of tilt and the maximum speed, we analyze the forces acting on the biker and bike system.

Let M be the total mass of the biker and bike.
Let u be the speed of the biker.
Let r be the radius of the turn.
Let g be the acceleration due to gravity.
Let $\theta$ be the angle of tilt from the vertical.

1. Angle of tilt ($\theta$)

When the biker executes a turn, the system (biker + bike) is subject to two main forces:

• Weight (Mg): Acting vertically downwards through the center of mass.
• Ground Reaction Force (R): This is the total force exerted by the ground on the bike's tires. It can be resolved into two components:
  • Normal force (N): Perpendicular to the ground. Since the road is horizontal, N acts vertically upwards.
  • Frictional force ($f_s$): Parallel to the ground, acting horizontally towards the center of the turn to provide the necessary centripetal force.

Alternatively, we can consider the total ground reaction force R. When the biker tilts at an angle $\theta$ from the vertical, the total ground reaction force R also makes an angle $\theta$ with the vertical.

Let's resolve the total ground reaction force R into its vertical and horizontal components:

• Vertical component: $R \cos \theta$. This component balances the weight of the biker and bike. $R \cos \theta = Mg \quad (1)$
• Horizontal component: $R \sin \theta$. This component provides the necessary centripetal force ($F_c = \frac{Mu^2}{r}$) for the circular motion. $R \sin \theta = \frac{Mu^2}{r} \quad (2)$

Dividing Equation (2) by Equation (1), we get: $\frac{R \sin \theta}{R \cos \theta} = \frac{Mu^2/r}{Mg}$ $\tan \theta = \frac{u^2}{rg}$ Therefore, the angle through which the biker has to tilt is: $\theta = \tan^{-1}\left(\frac{u^2}{rg}\right)$

2. Maximum Speed ($u_{max}$)

The maximum speed with which the biker can execute the turn is limited by the maximum static friction available between the tires and the road.
The horizontal component of the ground reaction force ($R \sin \theta$) is the static frictional force ($f_s$). $f_s = \frac{Mu^2}{r}$ The vertical component of the ground reaction force ($R \cos \theta$) is the normal force (N) that balances the weight. $N = Mg$ For the biker to execute the turn without skidding, the required static friction must be less than or equal to the maximum static friction: $f_s \le \mu_s N$ where $\mu_s$ is the coefficient of static friction between the tires and the road.

Substituting the expressions for $f_s$ and N: $\frac{Mu^2}{r} \le \mu_s Mg$ The mass M cancels out: $\frac{u^2}{r} \le \mu_s g$ For the maximum speed ($u_{max}$), the equality holds: $u_{max}^2 = \mu_s rg$ $u_{max} = \sqrt{\mu_s rg}$

This maximum speed is also related to the maximum possible tilt angle. The maximum angle of tilt ($\theta_{max}$) a biker can achieve without skidding is such that the angle of the total reaction force with the vertical is equal to the angle of friction ($\phi_s$), where $\tan \phi_s = \mu_s$. Thus, $\tan \theta_{max} = \mu_s$.
Using the banking equation: $\tan \theta_{max} = \frac{u_{max}^2}{rg}$ $\mu_s = \frac{u_{max}^2}{rg}$ $u_{max} = \sqrt{\mu_s rg}$ This confirms the result.

The assumption "Assume that the entire load of the bike is on the front wheel" is unusual for this type of problem. In the context of banking, it's typically ignored or implies that the center of mass is considered for the system. The standard derivation for banking angle and maximum speed based on friction does not change due to this specific wording, unless it implies a different physical model (e.g., specific stability limits or torques around a pivot). Assuming it's a simplification or a distractor, the standard physics approach is applied.