Question
Question: Which is smaller?: 2 or $(log_{e^{-1}}2 + log_{2}e^{-1})$...
Which is smaller?: 2 or (loge−12+log2e−1)
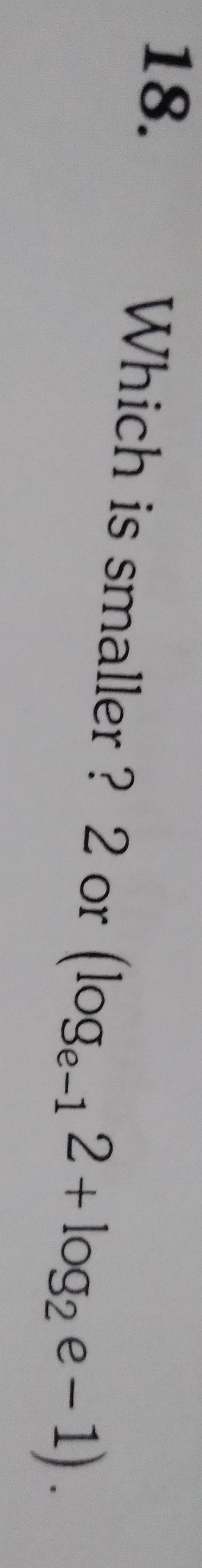
Answer
(loge−12+log2e−1)
Explanation
Solution
Let the given expression be E=loge−12+log2e−1. Using logarithm properties, E=−loge2−log2e. Let x=loge2. Then log2e=x1. So, E=−(x+x1). By AM-GM inequality, for x>0, x+x1≥2. Since x=loge2=1, x+x1>2. Therefore, E=−(x+x1)<−2. Since E<−2, E is smaller than 2.
