Question
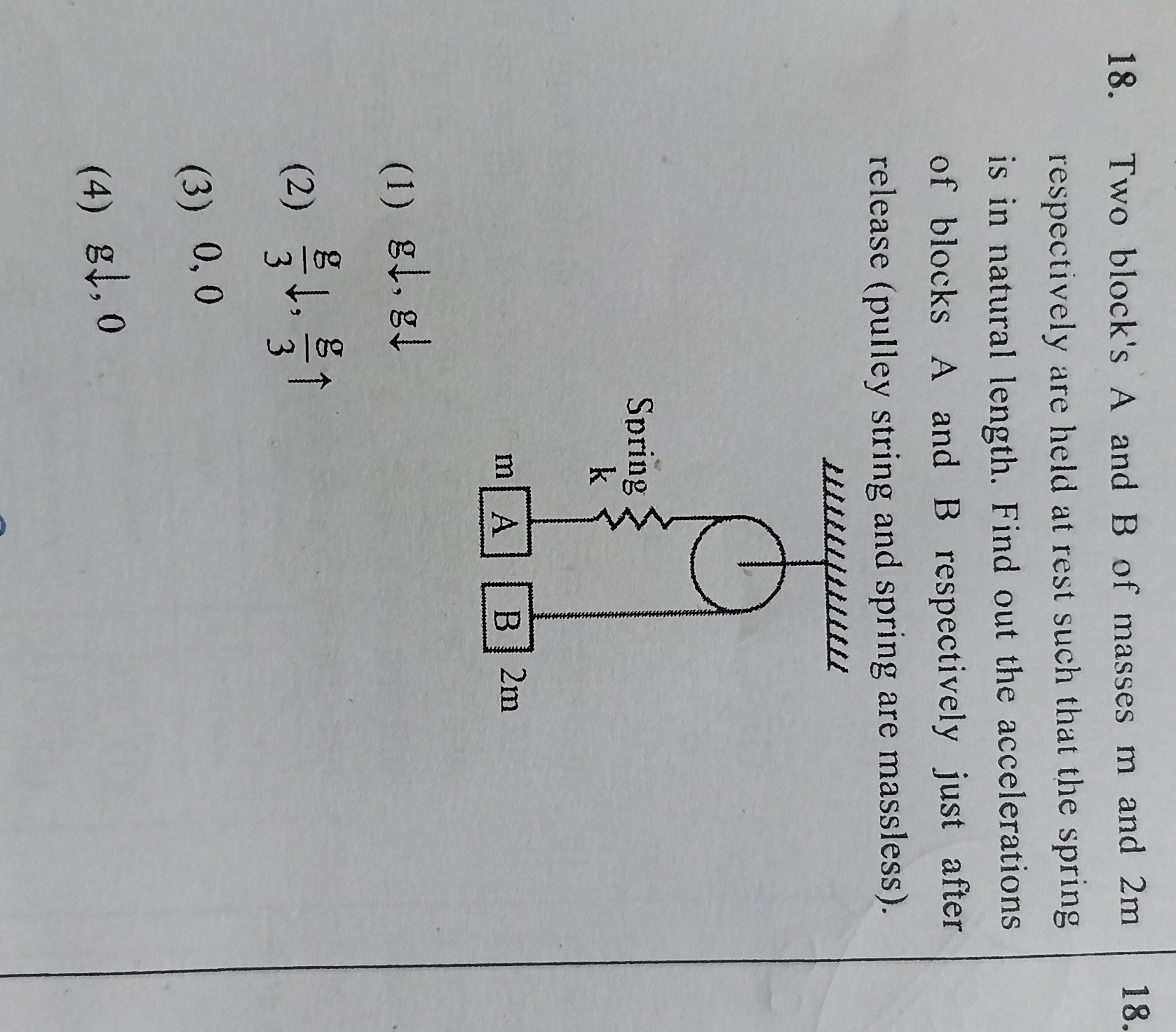
Question: Two block's A and B of masses m and 2m respectively are held at rest such that the spring is in natu...
Two block's A and B of masses m and 2m respectively are held at rest such that the spring is in natural length. Find out the accelerations of blocks A and B respectively just after release (pulley string and spring are massless).
3g↓,3g↑
g↓,g↓
0,0
g↓,0
3g↑,3g↓
Solution
Initially, the spring is at its natural length, so the spring force is zero. Let's analyze the forces on block A (mass m) and block B (mass 2m). We'll consider upward direction as positive.
For block B: The forces acting on B are gravity (downwards, 2mg) and tension from the string (upwards, T). The equation of motion for block B is: T−2mg=2maB (1)
For block A: The forces acting on A are gravity (downwards, mg), and tension from the string (upwards, T). The spring force is initially zero. The equation of motion for block A is: T−mg=maA (2)
Constraint relation: Since the string is inextensible and passes over a massless pulley, if block A moves up by a distance x, block B must move down by the same distance x. Therefore, their accelerations are related by aA=−aB.
Substitute aB=−aA into equation (1): T−2mg=2m(−aA) T−2mg=−2maA T=2mg−2maA
Now substitute this expression for T into equation (2): (2mg−2maA)−mg=maA mg−2maA=maA mg=3maA aA=3g
Since aA=3g, block A accelerates upwards with an acceleration of 3g. Using the constraint aB=−aA: aB=−3g
This means block B accelerates downwards with an acceleration of 3g.
Therefore, the accelerations of blocks A and B are 3g upwards and 3g downwards, respectively. This corresponds to 3g↑,3g↓. None of the provided options exactly match this result. Option (2) is 3g↓,3g↑, which has the directions reversed for both blocks. Assuming a typo in the options, the intended answer is likely derived from our calculation.
