Question

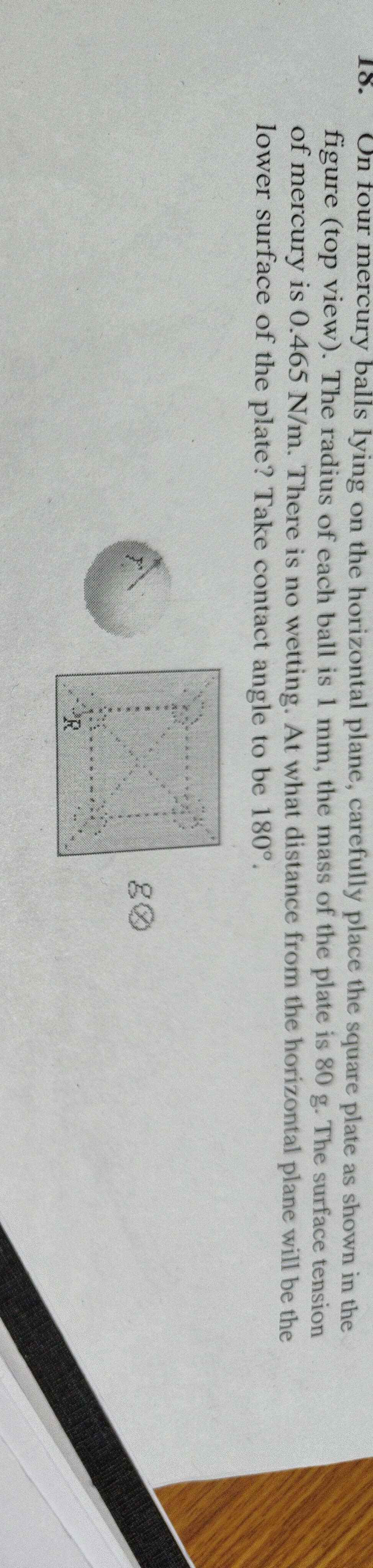
On four mercury balls lying on the horizontal plane, carefully place the square plate as shown in the figure (top view). The radius of each ball is 1 mm, the mass of the plate is 80 g. The surface tension of mercury is 0.465 N/m. There is no wetting. At what distance from the horizontal plane will be the lower surface of the plate? Take contact angle to be 180°.

• A. 1 mm
• B. 2 mm
• C. 4 mm
• D. 8 mm

Answer 1

Answer: (B)

2 mm

Answer 2

The problem asks for the distance from the horizontal plane to the lower surface of the plate. The plate is supported by four mercury balls. The weight of the plate is balanced by the upward force exerted by the mercury.

The weight of the plate is $W = mg$. Given $m = 80 \text{ g} = 0.08 \text{ kg}$ and $g \approx 9.8 \text{ m/s}^2$. $W = 0.08 \text{ kg} \times 9.8 \text{ m/s}^2 = 0.784 \text{ N}$.

The surface tension of mercury is $\gamma = 0.465 \text{ N/m}$, and the contact angle is $\theta = 180^\circ$. A contact angle of 180° signifies complete non-wetting, meaning the liquid (mercury) is repelled by the solid (plate).

The upward force supporting the plate is due to the surface tension acting along the perimeter of the plate where it contacts the mercury. Let the side length of the square plate be $a$. The perimeter of contact is $P = 4a$. The upward force due to surface tension is given by $F_{up} = \gamma P \cos \theta$. However, with $\theta = 180^\circ$, $\cos \theta = -1$, which would imply a downward force. This indicates that the standard formula for wetting needs careful interpretation for non-wetting conditions.

In cases of non-wetting ($\theta > 90^\circ$), the surface tension force acts to pull the liquid away from the solid. The resultant force on the solid due to surface tension can be upward if the liquid surface is curved away from the solid. For a plate resting on mercury balls with a 180° contact angle, the mercury surface is convex. The upward force is often approximated as $F_{up} = \gamma \times (\text{length of contact line})$.

Equating the weight of the plate to the upward force: $mg = \gamma \times P$ $0.784 \text{ N} = 0.465 \text{ N/m} \times 4a$ $a = \frac{0.784}{4 \times 0.465} \approx 0.4215 \text{ m}$.

The question asks for the distance from the horizontal plane to the lower surface of the plate. The mercury balls are on the horizontal plane, and their radius is $r = 1 \text{ mm}$. The plate is placed on these balls.

Since the contact angle is 180°, the mercury is repelled by the plate. The plate rests on the top of the mercury balls. The lowest point of each mercury ball is at height 0 (on the horizontal plane). The highest point of each mercury ball is at a height equal to its diameter, $2r$.

Assuming the plate rests on the top of these spherical balls without significant deformation or complex meniscus effects that would alter the height significantly, the lower surface of the plate will be at a height equal to the diameter of the mercury balls from the horizontal plane.

Distance from horizontal plane to lower surface of plate = Diameter of mercury ball $= 2r$. $h = 2 \times 1 \text{ mm} = 2 \text{ mm}$.