Question
Question: Minimum value of the expression $(4 \sin^2\theta + 12 \operatorname{cosec}^2\theta - 13)$ is equal t...
Minimum value of the expression (4sin2θ+12cosec2θ−13) is equal to-
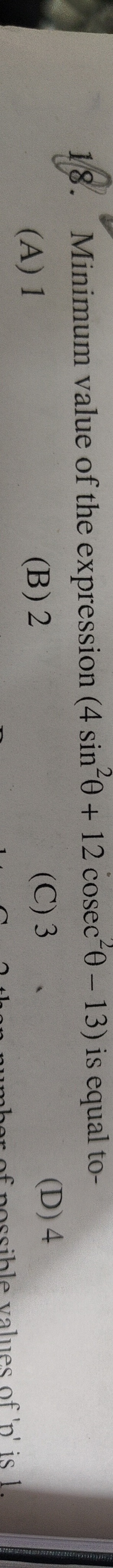
1
2
3
4
3
Solution
To find the minimum value of the expression (4sin2θ+12cosec2θ−13), let's analyze the term 4sin2θ+12cosec2θ.
-
Define a substitution: Let x=sin2θ. Since sinθ is a real number, 0≤sin2θ≤1. Also, for cosec2θ to be defined, sinθ=0, which means sin2θ=0. Therefore, the domain for x is x∈(0,1].
-
Rewrite the expression in terms of x: The expression becomes E=4x+12(x1)−13=4x+x12−13. We need to find the minimum value of this expression for x∈(0,1].
-
Analyze the function g(x)=4x+x12: To find the minimum value of g(x) on the interval (0,1], we can use calculus. Find the first derivative of g(x) with respect to x: g′(x)=dxd(4x+x12)=4−x212.
-
Determine the monotonicity of g(x) on (0,1]: For x∈(0,1], we have x2≤1. This implies x21≥1. Multiplying by 12, we get x212≥12. Now, consider g′(x)=4−x212. Since x212≥12, it follows that 4−x212≤4−12=−8. So, g′(x)≤−8, which means g′(x)<0 for all x∈(0,1].
-
Find the minimum value: Since g′(x)<0 on the interval (0,1], the function g(x) is strictly decreasing on this interval. For a strictly decreasing function, the minimum value occurs at the largest possible value in its domain. In this case, the largest value of x in (0,1] is x=1.
Substitute x=1 into g(x): g(1)=4(1)+112=4+12=16. This minimum value of g(x) occurs when sin2θ=1, which is a valid value (e.g., θ=2π).
-
Calculate the minimum value of the original expression: The minimum value of the expression (4sin2θ+12cosec2θ−13) is: Emin=g(1)−13=16−13=3.
