Question
Question: $\int \frac{e^x}{(2+e^x)(e^x+1)} dx =$ (where C is a constant of integration.)...
∫(2+ex)(ex+1)exdx=
(where C is a constant of integration.)
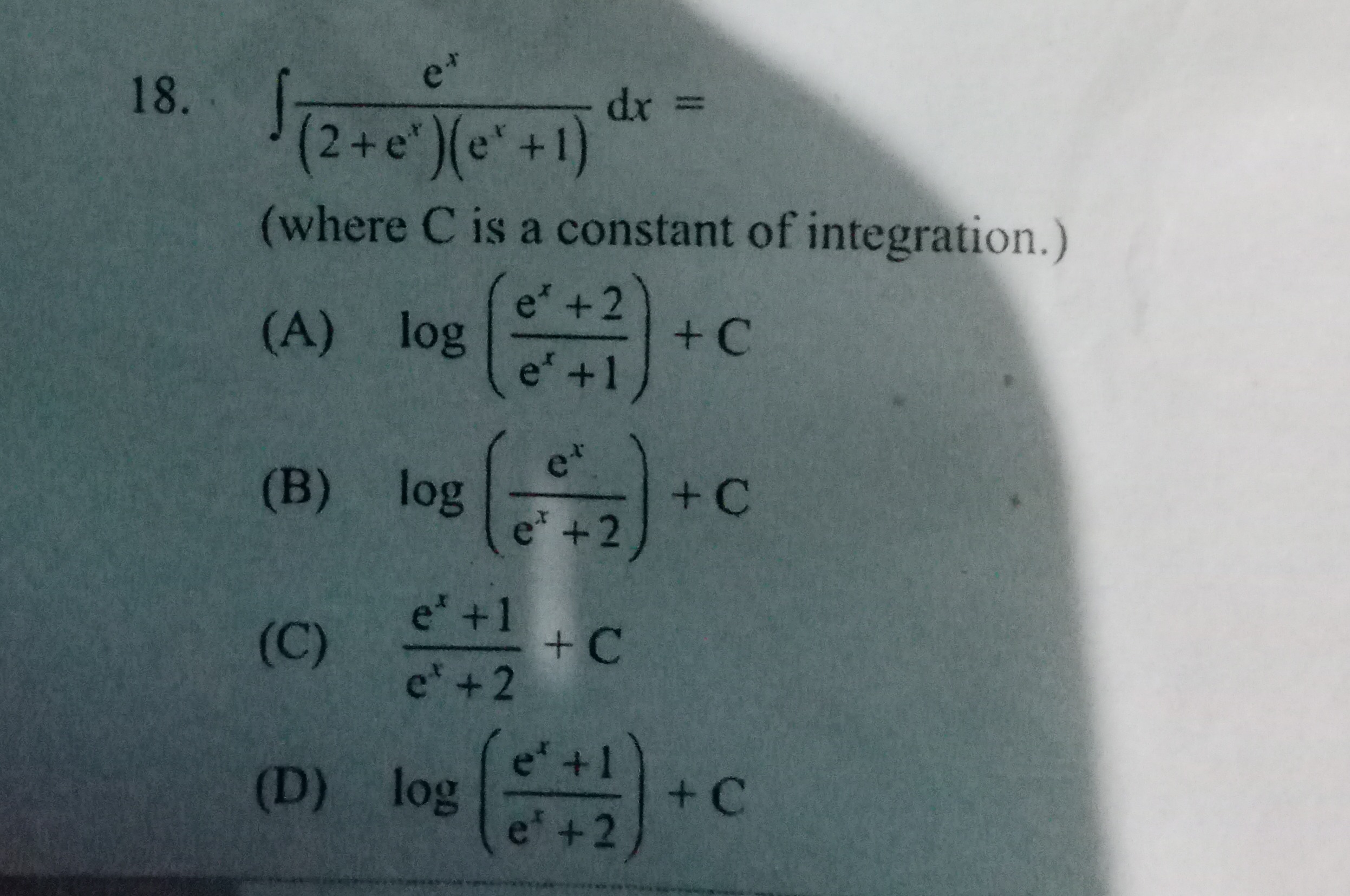
log(ex+1ex+2)+C
log(ex+2ex)+C
ex+2ex+1+C
log(ex+2ex+1)+C
ln(ex+2ex+1)+C
Solution
Let the given integral be I. I=∫(2+ex)(ex+1)exdx We use the substitution method. Let u=ex. Then, the differential du is given by du=dxd(ex)dx=exdx.
Substitute u and du into the integral: I=∫(2+u)(u+1)du Now, we have a rational function in terms of u. We can solve this integral using partial fraction decomposition. We decompose the integrand (u+2)(u+1)1 into partial fractions: (u+2)(u+1)1=u+2A+u+1B To find the constants A and B, we multiply both sides by (u+2)(u+1): 1=A(u+1)+B(u+2) Set u=−1: 1=A(−1+1)+B(−1+2) 1=A(0)+B(1) 1=B Set u=−2: 1=A(−2+1)+B(−2+2) 1=A(−1)+B(0) 1=−A A=−1 So, the partial fraction decomposition is: (u+2)(u+1)1=u+2−1+u+11 Now, we can rewrite the integral as: I=∫(u+11−u+21)du Integrate each term: I=∫u+11du−∫u+21du I=ln∣u+1∣−ln∣u+2∣+C Using the property of logarithms lna−lnb=lnba: I=lnu+2u+1+C Finally, substitute back u=ex: I=lnex+2ex+1+C Since ex>0 for all real x, both ex+1 and ex+2 are positive. Thus, the absolute value is not necessary. I=ln(ex+2ex+1)+C
The final answer is ln(ex+2ex+1)+C.
