Question

In a triangle ABC if $\frac{sin^2 A + sin^2 B + sin^2 C}{cos^2 A + cos^2 B + cos^2 C} = 2$; then-

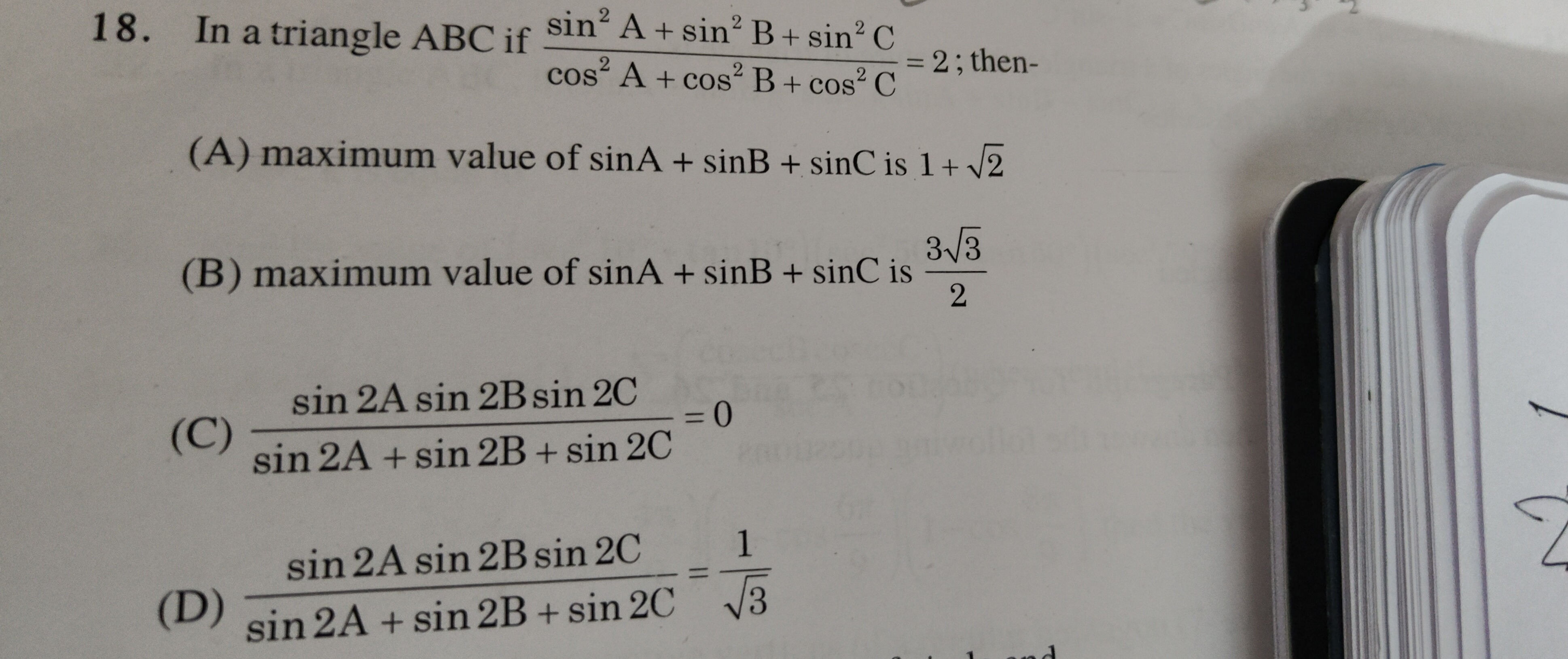
• A. maximum value of sinA + sinB + sinC is $1 + \sqrt{2}$
• B. maximum value of sinA + sinB + sinC is $\frac{3\sqrt{3}}{2}$
• C. $\frac{sin 2A sin 2B sin 2C}{sin 2A + sin 2B + sin 2C} = 0$
• D. $\frac{sin 2A sin 2B sin 2C}{sin 2A + sin 2B + sin 2C} = \frac{1}{\sqrt{3}}$

Answer 1

Answer: (A), (C)

Options (A) and (C) are correct.

Answer 2

The given condition is $\frac{sin^2 A + sin^2 B + sin^2 C}{cos^2 A + cos^2 B + cos^2 C} = 2$.

Let's simplify the denominator using $cos^2 X = 1 - sin^2 X$: $cos^2 A + cos^2 B + cos^2 C = (1 - sin^2 A) + (1 - sin^2 B) + (1 - sin^2 C)$ $= 3 - (sin^2 A + sin^2 B + sin^2 C)$.

Substitute this into the given equation: $\frac{sin^2 A + sin^2 B + sin^2 C}{3 - (sin^2 A + sin^2 B + sin^2 C)} = 2$.

Let $X = sin^2 A + sin^2 B + sin^2 C$. $\frac{X}{3 - X} = 2$ $X = 2(3 - X)$ $X = 6 - 2X$ $3X = 6$ $X = 2$.

So, we have $sin^2 A + sin^2 B + sin^2 C = 2$. Consequently, $cos^2 A + cos^2 B + cos^2 C = 3 - X = 3 - 2 = 1$.

Now, let's use the identity $cos^2 \theta = \frac{1 + cos 2\theta}{2}$: $cos^2 A + cos^2 B + cos^2 C = 1$ $\frac{1 + cos 2A}{2} + \frac{1 + cos 2B}{2} + \frac{1 + cos 2C}{2} = 1$ $1 + cos 2A + 1 + cos 2B + 1 + cos 2C = 2$ $3 + cos 2A + cos 2B + cos 2C = 2$ $cos 2A + cos 2B + cos 2C = -1$.

For a triangle ABC, we have the identity $cos 2A + cos 2B + cos 2C = -1 - 4 cos A cos B cos C$. Substituting this into the equation above: $-1 - 4 cos A cos B cos C = -1$ $-4 cos A cos B cos C = 0$ $cos A cos B cos C = 0$.

This implies that at least one of $cos A$, $cos B$, or $cos C$ must be zero. Since A, B, C are angles of a triangle ($0 < A, B, C < \pi$), if $cos X = 0$, then $X = \frac{\pi}{2} = 90^\circ$. Therefore, the triangle ABC must be a right-angled triangle.

Now let's evaluate the given options:

(A) maximum value of sinA + sinB + sinC is $1 + \sqrt{2}$ Since the triangle is right-angled, let's assume $A = 90^\circ$. Then $B+C = 90^\circ$. The expression becomes $sin 90^\circ + sin B + sin C = 1 + sin B + sin (90^\circ - B)$ $= 1 + sin B + cos B$. To find the maximum value of $1 + sin B + cos B$, we need to maximize $sin B + cos B$. $sin B + cos B = \sqrt{2} \left(\frac{1}{\sqrt{2}} sin B + \frac{1}{\sqrt{2}} cos B\right)$ $= \sqrt{2} \left(cos \frac{\pi}{4} sin B + sin \frac{\pi}{4} cos B\right)$ $= \sqrt{2} sin \left(B + \frac{\pi}{4}\right)$. The maximum value of $sin \left(B + \frac{\pi}{4}\right)$ is $1$. This occurs when $B + \frac{\pi}{4} = \frac{\pi}{2}$, so $B = \frac{\pi}{4} = 45^\circ$. If $B = 45^\circ$, then $C = 90^\circ - 45^\circ = 45^\circ$. The maximum value of $sin A + sin B + sin C$ is $1 + \sqrt{2} \times 1 = 1 + \sqrt{2}$. Thus, option (A) is correct.

(B) maximum value of sinA + sinB + sinC is $\frac{3\sqrt{3}}{2}$ This value corresponds to an equilateral triangle where $A=B=C=60^\circ$. However, we found that the triangle must be right-angled. An equilateral triangle is not right-angled. Also, for an equilateral triangle, $sin^2 A + sin^2 B + sin^2 C = 3(\frac{\sqrt{3}}{2})^2 = \frac{9}{4}$ and $cos^2 A + cos^2 B + cos^2 C = 3(\frac{1}{2})^2 = \frac{3}{4}$. The ratio is $\frac{9/4}{3/4} = 3$, which is not $2$. Thus, option (B) is incorrect.

(C) $\frac{sin 2A sin 2B sin 2C}{sin 2A + sin 2B + sin 2C} = 0$ Since the triangle is right-angled, let $A = 90^\circ$. Then $2A = 180^\circ$. So, $sin 2A = sin 180^\circ = 0$. The numerator of the expression is $sin 2A sin 2B sin 2C = 0 \times sin 2B \times sin 2C = 0$. Now consider the denominator: $sin 2A + sin 2B + sin 2C = 0 + sin 2B + sin 2C$. Since $B+C = 90^\circ$, $C = 90^\circ - B$. $sin 2B + sin 2C = sin 2B + sin (2(90^\circ - B)) = sin 2B + sin (180^\circ - 2B)$ $= sin 2B + sin 2B = 2 sin 2B$. Since $B$ is an angle of a right-angled triangle, $0 < B < 90^\circ$. Therefore, $0 < 2B < 180^\circ$, which means $sin 2B > 0$. So, the denominator $2 sin 2B \neq 0$. Therefore, $\frac{sin 2A sin 2B sin 2C}{sin 2A + sin 2B + sin 2C} = \frac{0}{2 sin 2B} = 0$. Thus, option (C) is correct.

(D) $\frac{sin 2A sin 2B sin 2C}{sin 2A + sin 2B + sin 2C} = \frac{1}{\sqrt{3}}$ Based on the calculation for option (C), this option is incorrect.

Both options (A) and (C) are correct.