Question

If $\vec{a} = i + j + k$, $\vec{c} = j - k$, $\vec{a} \times \vec{b} = \vec{c}$ and $\vec{a}.\vec{b} = 1$ then $\vec{b} =$

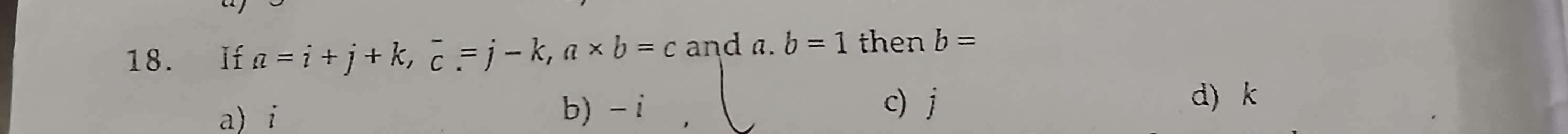
• A. i
• B.
  • i
• C. j
• D. k

Answer 1

Answer: (A)

i

Answer 2

Let $\vec{b} = xi + yj + zk$.

Given:

$$\vec{a} = i + j + k, \quad \vec{c} = j - k, \quad \vec{a} \times \vec{b} = \vec{c}, \quad \vec{a} \cdot \vec{b} = 1.$$

Step 1: Dot Product Condition

$$\vec{a} \cdot \vec{b} = x + y + z = 1. \quad \text{(1)}$$

Step 2: Cross Product Condition

$$\vec{a} \times \vec{b} = \begin{vmatrix} i & j & k \\ 1 & 1 & 1 \\ x & y & z \end{vmatrix} = i(z - y) - j(z - x) + k(y - x).$$

We are given:

$$\vec{a} \times \vec{b} = 0\,i + 1\,j - 1\,k.$$

Thus, equating components:

$$\begin{cases} z - y = 0, \quad \text{(i-component)}\\[1mm] -(z - x) = 1 \quad \Rightarrow \quad z - x = -1,\\[1mm] y - x = -1. \end{cases}$$

From $z - y = 0$, we have:

$$y = z. \quad \text{(2)}$$

From $y - x = -1$, substituting $y=z$ gives:

$$z - x = -1 \quad \Rightarrow \quad x = z + 1. \quad \text{(3)}$$

(This is consistent with the second equation.)

Step 3: Solve Using Dot Product Substitute $x$ and $y$ from (2) and (3) into equation (1):

$$(z + 1) + z + z = 1 \quad \Rightarrow \quad 3z + 1 = 1 \quad \Rightarrow \quad 3z = 0 \quad \Rightarrow \quad z = 0.$$

Then:

$$y = z = 0,\quad x = 0 + 1 = 1.$$

Thus,

$$\vec{b} = i.$$