Question

$\frac{(x-1)(x+1)(x-2)^2(e^{3x}-1)}{x(3-x)^3(x-1)^2(x+3)} <0$

Answer 1

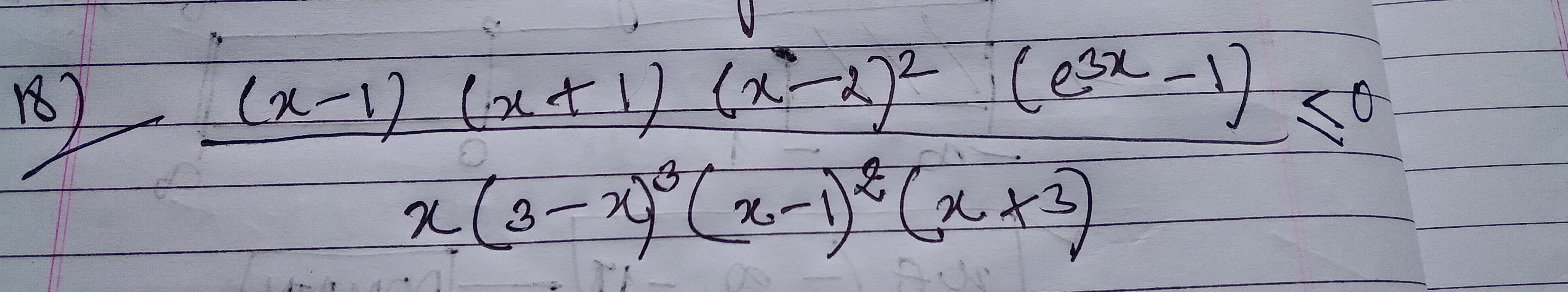
(-1, 0) \cup (0, 1) \cup (3, \infty)

Answer 2

The inequality is $\frac{(x-1)(x+1)(x-2)^2(e^{3x}-1)}{x(3-x)^3(x-1)^2(x+3)} <0$. First, identify the critical points by setting the numerator and denominator to zero. Numerator zeros: $x-1=0 \implies x=1$, $x+1=0 \implies x=-1$, $(x-2)^2=0 \implies x=2$, $e^{3x}-1=0 \implies e^{3x}=1 \implies 3x=0 \implies x=0$. Denominator zeros: $x=0$, $3-x=0 \implies x=3$, $(x-1)^2=0 \implies x=1$, $x+3=0 \implies x=-3$. The expression is undefined at $x \in \{-3, 0, 1, 3\}$. The expression is zero at $x \in \{-1, 0, 1, 2\}$. Since the inequality is strict ($<0$), these values are not part of the solution. The simplified set of critical points to consider for sign changes are $x \in \{-3, -1, 0, 1, 2, 3\}$.

Simplify the inequality by canceling common factors: $\frac{(x-1)(x+1)(x-2)^2(e^{3x}-1)}{x(3-x)^3(x-1)^2(x+3)} = \frac{(x+1)(x-2)^2(e^{3x}-1)}{x(3-x)^3(x-1)(x+3)}$ for $x \neq 1$.

Now analyze the sign of the simplified expression $P(x) = \frac{(x+1)(x-2)^2(e^{3x}-1)}{x(3-x)^3(x-1)(x+3)}$ in the intervals defined by the critical points: $(-\infty, -3)$, $(-3, -1)$, $(-1, 0)$, $(0, 1)$, $(1, 2)$, $(2, 3)$, $(3, \infty)$.

• $(x-2)^2$ is always positive for $x \neq 2$.
• $(e^{3x}-1)$ is negative for $x<0$ and positive for $x>0$.
• $(3-x)^3$ has the same sign as $(3-x)$. It's positive for $x<3$ and negative for $x>3$.

Let's examine the sign of $P(x)$ in each interval:

1. Interval $(-\infty, -3)$: Let $x=-4$. $P(-4) = \frac{(-3)(+)(e^{-12}-1)}{(-4)(-7)^3(-5)(-1)} = \frac{(-)(+)(-)}{(-)(-)(-)(-)} = \frac{+}{+} = +$
2. Interval $(-3, -1)$: Let $x=-2$. $P(-2) = \frac{(-1)(+)(e^{-6}-1)}{(-2)(-5)^3(-3)(-1)} = \frac{(-)(+)(-)}{(-)(-)(-)(-)} = \frac{+}{+} = +$
3. Interval $(-1, 0)$: Let $x=-0.5$. $P(-0.5) = \frac{(+)(+)(e^{-1.5}-1)}{(-0.5)(3.5)^3(-1.5)(2.5)} = \frac{(+)(+)(-)}{(-)(+)(-)(+)} = \frac{-}{+} = -$
4. Interval $(0, 1)$: Let $x=0.5$. $P(0.5) = \frac{(1.5)(+)(e^{1.5}-1)}{(0.5)(2.5)^3(-0.5)(3.5)} = \frac{(+)(+)(+)}{(+)(+)(-)(+)} = \frac{+}{-} = -$
5. Interval $(1, 2)$: Let $x=1.5$. $P(1.5) = \frac{(2.5)(+)(e^{4.5}-1)}{(1.5)(1.5)^3(0.5)(4.5)} = \frac{(+)(+)(+)}{(+)(+)(+)(+)} = \frac{+}{+} = +$
6. Interval $(2, 3)$: Let $x=2.5$. $P(2.5) = \frac{(3.5)(+)(e^{7.5}-1)}{(2.5)(0.5)^3(1.5)(5.5)} = \frac{(+)(+)(+)}{(+)(+)(+)(+)} = \frac{+}{+} = +$
7. Interval $(3, \infty)$: Let $x=4$. $P(4) = \frac{(5)(+)(e^{12}-1)}{(4)(-1)^3(3)(7)} = \frac{(+)(+)(+)}{(+)(-)(+)(+)} = \frac{+}{-} = -$

The inequality $P(x) < 0$ is satisfied for $x \in (-1, 0) \cup (0, 1) \cup (3, \infty)$. The critical points $x=-3, -1, 0, 1, 2, 3$ are excluded because the inequality is strict or because they make the denominator zero. The term $(x-2)^2$ being zero at $x=2$ results in the expression being 0, which is not less than 0. The term $(e^{3x}-1)$ being zero at $x=0$ also results in the expression being 0. The common factor $(x-1)$ being zero at $x=1$ results in a 0/0 form, and after simplification, $x=1$ is a root of the denominator, so it's excluded.

Therefore, the solution set is $(-1, 0) \cup (0, 1) \cup (3, \infty)$.