Question
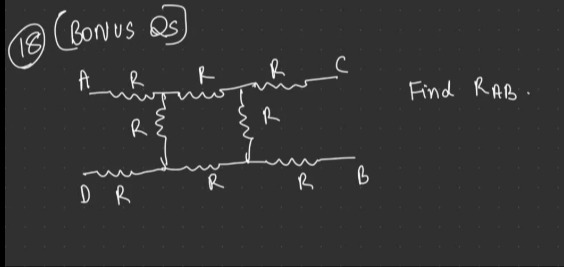
Question: Find $R_{AB}$....
Find RAB.
3R
Solution
To find the equivalent resistance RAB for the given circuit, we first analyze the circuit structure and identify any open ends.
-
Identify Open Ends: The problem asks for RAB, implying that current enters at A and exits at B. Points C and D are the ends of the top and bottom branches, respectively. Since nothing is connected to C and D, they are considered open circuits. This means no current flows through the resistor connected between Q and C, and no current flows through the resistor connected between D and S. Therefore, these two resistors can be removed from the circuit for the calculation of RAB.
-
Redraw the Simplified Circuit: After removing the resistors R(Q-C) and R(D-S), the circuit simplifies to:
-
Identify Series/Parallel Combinations: The circuit can be viewed as three parts in series:
- Resistor between A and P (RAP=R).
- A bridge-like network between P and T.
- Resistor between T and B (RTB=R).
-
Simplify the Bridge Network (P-Q-S-T): Consider the section of the circuit between points P and T. This section consists of four resistors: R(P-Q), R(P-S), R(Q-T), and R(S-T). We can see two parallel paths from P to T:
- Path 1: P → Q → T. The total resistance of this path is RPQT=RPQ+RQT=R+R=2R.
- Path 2: P → S → T. The total resistance of this path is RPST=RPS+RST=R+R=2R.
Since these two paths are in parallel between P and T, their equivalent resistance (RPT) is: RPT=RPQT+RPSTRPQT×RPST=2R+2R2R×2R=4R4R2=R
-
Calculate Total Equivalent Resistance RAB: Now, the entire circuit is a series combination of RAP, RPT, and RTB: RAB=RAP+RPT+RTB RAB=R+R+R RAB=3R
The final answer is 3R.
Explanation of the solution:
- Identify open ends C and D; remove resistors R(Q-C) and R(D-S).
- The circuit simplifies to A-R-P, a bridge network P-T, and T-R-B.
- The bridge network (P-Q-T and P-S-T) consists of two parallel branches, each with resistance 2R. Their equivalent resistance is RPT=(2R×2R)/(2R+2R)=R.
- The total equivalent resistance RAB is the series combination of R(A-P), RPT, and R(T-B), which is R+R+R=3R.
Answer: 3R
