Solveeit Logo
Login

Question

Question: A square loop of side 'a' carries a current $I$. It is placed as shown in figure. Magnetic moment of...

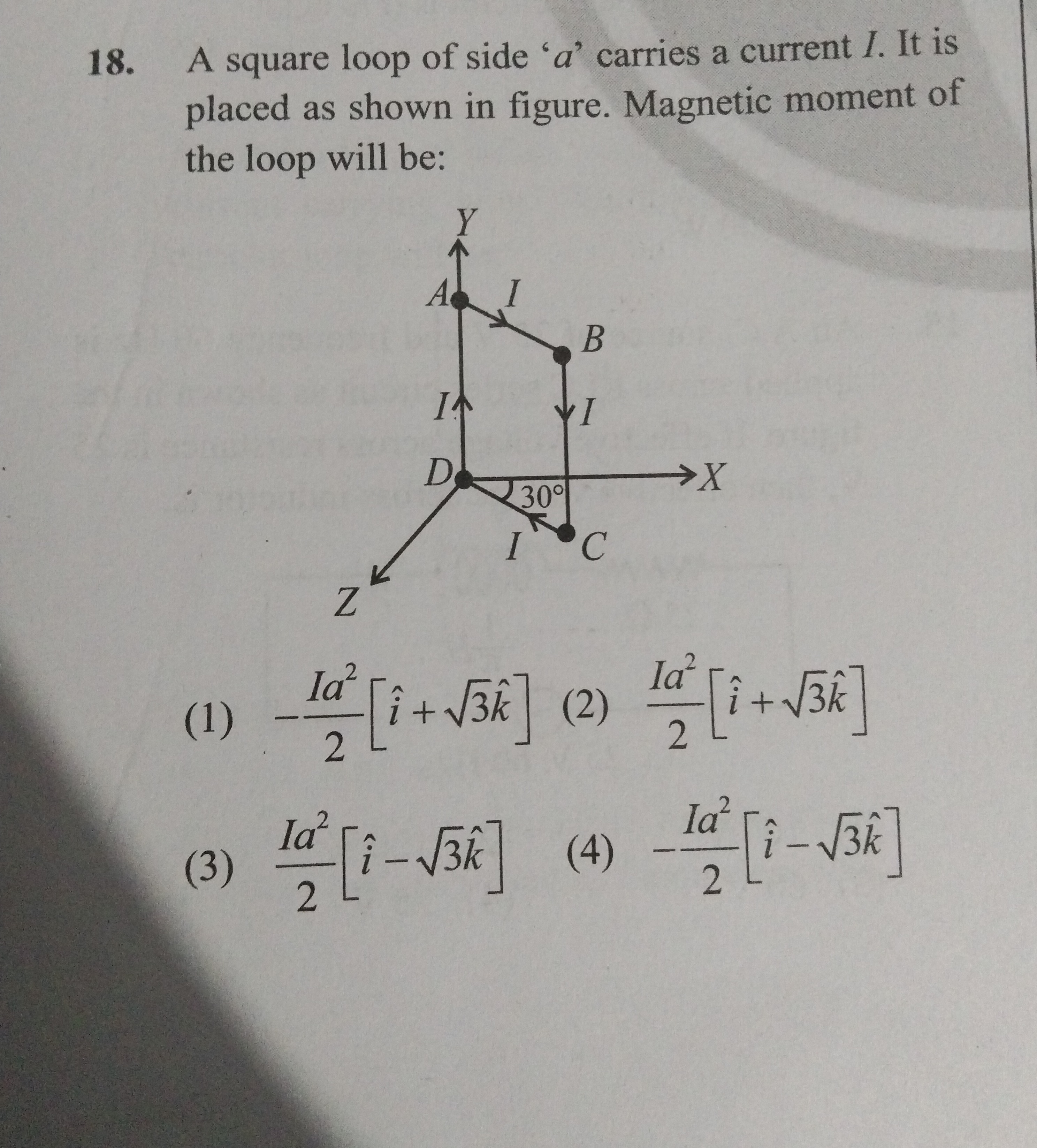
A square loop of side 'a' carries a current II. It is placed as shown in figure. Magnetic moment of the loop will be:

A

−Ia22[i^+3k^]-\frac{Ia^2}{2}[\hat{i} + \sqrt{3}\hat{k}]

B

Ia22[i^+3k^]\frac{Ia^2}{2}[\hat{i} + \sqrt{3}\hat{k}]

C

Ia22[i^−3k^]\frac{Ia^2}{2}[\hat{i} - \sqrt{3}\hat{k}]

D

−Ia22[i^−3k^]-\frac{Ia^2}{2}[\hat{i} - \sqrt{3}\hat{k}]

Answer

Ia22[i^−3k^]\frac{Ia^2}{2}[\hat{i} - \sqrt{3}\hat{k}]

Explanation

Solution

  1. Identify two adjacent sides at vertex A using the loop order (current flows A → B → C → D). Choose:

    • DA = A – D = (0, a, 0)
    • AB = B – A = (a cos 30°, 0, a sin 30°) = (a3/2,0,a/2)(a\sqrt{3}/2, 0, a/2)

  2. The vector area (with magnitude equal to the area of the square and direction given by the right‐hand rule) is given by

    A⃗=DA×AB.\vec{A} = \textbf{DA} \times \textbf{AB}.

  3. Compute the cross product:

    A⃗=(0,a,0)×(a32,0,a2)=(a⋅a2−0,  0−0,  0−a⋅a32)=(a22, 0, −a232).\vec{A} = (0,a,0) \times \left(\frac{a\sqrt{3}}{2},0,\frac{a}{2}\right) = \left(a \cdot \frac{a}{2} - 0,\; 0 - 0,\; 0 - a \cdot \frac{a\sqrt{3}}{2}\right) = \left(\frac{a^2}{2},\, 0,\, -\frac{a^2\sqrt{3}}{2}\right).

  4. The magnetic moment is

    M⃗=I A⃗=I a22 (i^−3 k^).\vec{M} = I\,\vec{A} = \frac{I\,a^2}{2}\,(\hat{i} - \sqrt{3}\,\hat{k}).