Question

A ball dropped from a height $H$ strikes a frictionless inclined plane at a height $h$ as shown in the figure. The plane is inclined at angle $\theta$ with the horizontal. As a result of the collision, the direction of the ball becomes horizontal.

Answer 1

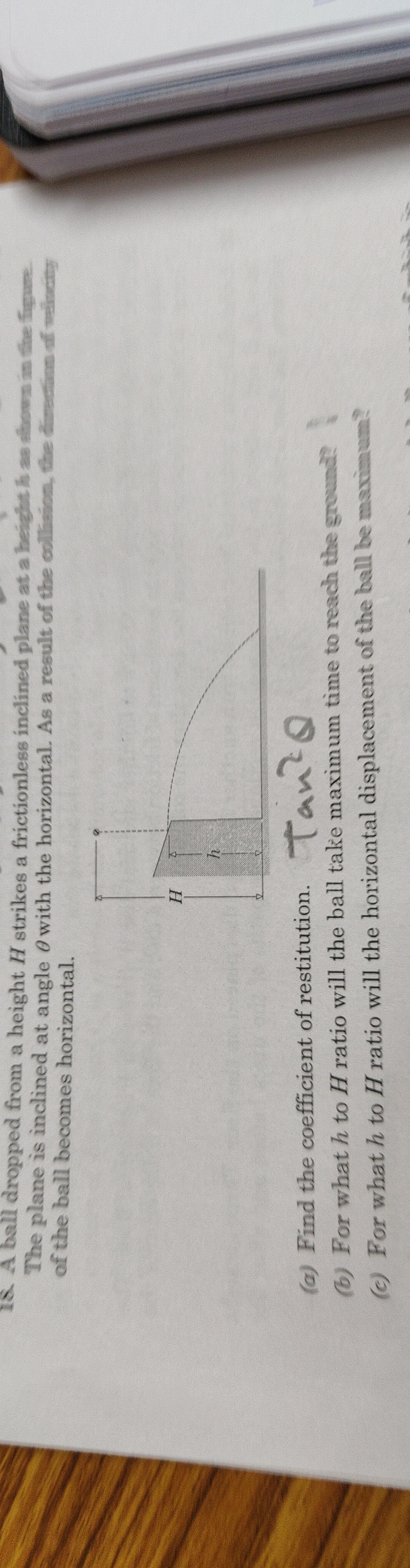
a) $\tan^2\theta$, b) $h/H = 1/2$, c) $h/H = 1/2$

Answer 2

The problem involves a ball dropped from a height, colliding with a frictionless inclined plane, and then undergoing projectile motion. We need to analyze the collision and subsequent motion to answer the three parts.

Given:

• Initial height of drop: $H$
• Height of the inclined plane from the ground: $h$
• Angle of inclination of the plane with the horizontal: $\theta$
• Collision is frictionless.
• After collision, the direction of the ball becomes horizontal.

Step-by-step Derivations:

1. Velocity of the ball just before collision:

The ball falls freely from height $H$ to $h$, covering a vertical distance of $(H-h)$. Let $v_0$ be the speed of the ball just before it strikes the inclined plane. Using the equation $v^2 = u^2 + 2as$: $v_0^2 = 0^2 + 2g(H-h)$ $v_0 = \sqrt{2g(H-h)}$ The direction of $v_0$ is vertically downwards.

Part (a): Find the coefficient of restitution ($e$).

For a frictionless collision, the component of velocity parallel to the plane remains unchanged. The coefficient of restitution relates the normal components of velocities.

Let's define a coordinate system: x-axis horizontal, y-axis vertical upwards. The inclined plane makes an angle $\theta$ with the horizontal. The normal to the plane (pointing outwards from the plane) makes an angle $(90^\circ - \theta)$ with the horizontal or an angle $\theta$ with the vertical.

• Velocity before collision: $\vec{v}_{before} = (0, -v_0)$.

  • Component of $\vec{v}_{before}$ parallel to the plane: $v_{||, before} = v_0 \sin\theta$. (This is the component along the plane, downwards).
  • Component of $\vec{v}_{before}$ perpendicular to the plane (approaching): $v_{\perp, before} = v_0 \cos\theta$. (This is the component into the plane).

• Velocity after collision: The problem states the direction of the ball becomes horizontal. Let the speed be $v_H$. $\vec{v}_{after} = (v_H, 0)$.

  • Component of $\vec{v}_{after}$ parallel to the plane: $v_{||, after} = v_H \cos\theta$. (This is the component along the plane, downwards).
  • Component of $\vec{v}_{after}$ perpendicular to the plane (separating): $v_{\perp, after} = v_H \sin\theta$. (This is the component away from the plane).

• Conservation of parallel component of velocity: Since the plane is frictionless, $v_{||, after} = v_{||, before}$. $v_H \cos\theta = v_0 \sin\theta$ $v_H = v_0 \frac{\sin\theta}{\cos\theta} = v_0 \tan\theta$.

• Coefficient of restitution ($e$): $e = \frac{\text{speed of separation along normal}}{\text{speed of approach along normal}}$ $e = \frac{v_{\perp, after}}{v_{\perp, before}} = \frac{v_H \sin\theta}{v_0 \cos\theta}$ Substitute $v_H = v_0 \tan\theta$: $e = \frac{(v_0 \tan\theta) \sin\theta}{v_0 \cos\theta} = \frac{\tan\theta \sin\theta}{\cos\theta} = \frac{(\sin\theta/\cos\theta) \sin\theta}{\cos\theta} = \frac{\sin^2\theta}{\cos^2\theta} = \tan^2\theta$.

Part (b): For what $h$ to $H$ ratio will the ball take maximum time to reach the ground?

The total time to reach the ground ($T_{total}$) consists of two parts:

1. Time to fall from height $H$ to $h$ ($t_1$).
2. Time for projectile motion from height $h$ to the ground ($t_2$).

• Time $t_1$: $H-h = \frac{1}{2}gt_1^2 \implies t_1 = \sqrt{\frac{2(H-h)}{g}}$.

• Time $t_2$: After collision, the ball is at height $h$ and has a horizontal velocity $v_H$. Its initial vertical velocity is 0. $h = 0 \cdot t_2 + \frac{1}{2}gt_2^2 \implies t_2 = \sqrt{\frac{2h}{g}}$.

• Total time $T_{total}$: $T_{total} = t_1 + t_2 = \sqrt{\frac{2(H-h)}{g}} + \sqrt{\frac{2h}{g}}$ To find the ratio $h/H$ for maximum $T_{total}$, we differentiate $T_{total}$ with respect to $h$ and set it to zero. Let $C = \sqrt{2/g}$. Then $T_{total} = C(\sqrt{H-h} + \sqrt{h})$. $\frac{dT_{total}}{dh} = C \left( \frac{1}{2\sqrt{H-h}}(-1) + \frac{1}{2\sqrt{h}}(1) \right) = 0$ $\frac{1}{\sqrt{h}} = \frac{1}{\sqrt{H-h}}$ $\sqrt{h} = \sqrt{H-h}$ Squaring both sides: $h = H-h \implies 2h = H \implies h = H/2$. Thus, the ratio $h/H = 1/2$.

Part (c): For what $h$ to $H$ ratio will the horizontal displacement of the ball be maximum?

The horizontal displacement ($X$) occurs during the projectile motion after collision. $X = v_H \cdot t_2$ We have $v_H = \sqrt{2g(H-h)} \tan\theta$ and $t_2 = \sqrt{\frac{2h}{g}}$. $X = \left(\sqrt{2g(H-h)} \tan\theta\right) \left(\sqrt{\frac{2h}{g}}\right)$ $X = \sqrt{2g(H-h) \cdot \frac{2h}{g}} \tan\theta$ $X = \sqrt{4h(H-h)} \tan\theta$ $X = 2 \tan\theta \sqrt{h(H-h)}$

To maximize $X$, we need to maximize the term $\sqrt{h(H-h)}$, which is equivalent to maximizing $f(h) = h(H-h)$. $f(h) = Hh - h^2$. To find the maximum, differentiate $f(h)$ with respect to $h$ and set it to zero: $\frac{df}{dh} = H - 2h = 0$ $2h = H \implies h = H/2$. Thus, the ratio $h/H = 1/2$.

Summary of Answers:

(a) The coefficient of restitution is $e = \tan^2\theta$. (b) The ratio $h/H$ for which the ball will take maximum time to reach the ground is $1/2$. (c) The ratio $h/H$ for which the horizontal displacement of the ball will be maximum is $1/2$.

Explanation of the solution:

(a) The collision is frictionless, so the velocity component parallel to the inclined plane is conserved. The initial velocity is vertical ($v_0 = \sqrt{2g(H-h)}$), and the final velocity is horizontal ($v_H$). By resolving initial and final velocities into components parallel and perpendicular to the plane, and applying conservation of parallel component and the definition of coefficient of restitution ($e = \frac{\text{relative speed of separation}}{\text{relative speed of approach}}$ along the normal), we find $e = \tan^2\theta$.

(b) The total time is the sum of time to fall to height $h$ and time for projectile motion from height $h$. $T_{total} = \sqrt{\frac{2(H-h)}{g}} + \sqrt{\frac{2h}{g}}$. To maximize this, we differentiate with respect to $h$ and set to zero, yielding $h=H/2$.

(c) The horizontal displacement is the product of the horizontal velocity after collision ($v_H = \sqrt{2g(H-h)}\tan\theta$) and the time of flight from height $h$ ($t_2 = \sqrt{\frac{2h}{g}}$). This gives $X = 2\tan\theta\sqrt{h(H-h)}$. Maximizing $h(H-h)$ by differentiation with respect to $h$ gives $h=H/2$.