Question

What volume (in ml) of 0.8 M $AlCl_3$ solution to get solution of chloride ion concentration equal to 0.6 M ?

Answer 1

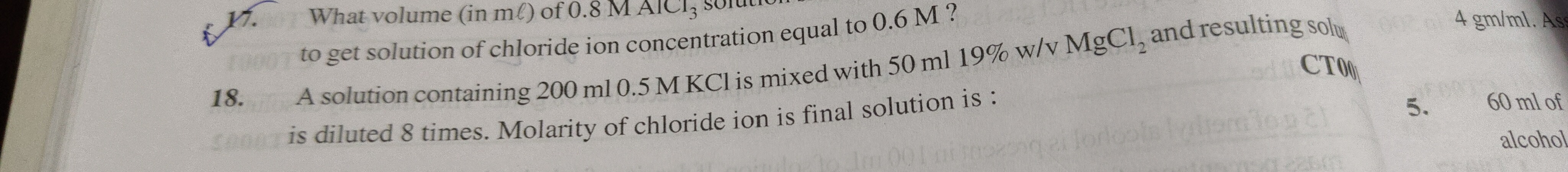
250 ml

Answer 2

The question asks for a specific volume of a concentrated $AlCl_3$ solution required to prepare a solution with a desired chloride ion concentration. To obtain a numerical answer for volume, we must assume a final target volume for the solution to be prepared. A standard assumption in such cases is to prepare 1 liter (1000 ml) of the final solution.

1. Determine moles of chloride ions needed in the final solution: We want a final solution with a chloride ion concentration of 0.6 M. If we assume the final volume is 1 L (1000 ml): $\text{Moles of } Cl^- \text{ needed} = \text{Molarity} \times \text{Volume (in L)} = 0.6 \text{ mol/L} \times 1 \text{ L} = 0.6 \text{ mol}$

2. Relate moles of chloride ions to moles of $AlCl_3$: Aluminum chloride ($AlCl_3$) dissociates in water as follows: $AlCl_3 (aq) \rightarrow Al^{3+} (aq) + 3Cl^- (aq)$ This means 1 mole of $AlCl_3$ produces 3 moles of $Cl^-$ ions. Therefore, to get 0.6 moles of $Cl^-$, we need: $\text{Moles of } AlCl_3 \text{ required} = \frac{\text{Moles of } Cl^- \text{ needed}}{3} = \frac{0.6 \text{ mol}}{3} = 0.2 \text{ mol}$

3. Calculate the volume of the 0.8 M $AlCl_3$ stock solution: We have a stock solution of 0.8 M $AlCl_3$. To find the volume containing 0.2 moles of $AlCl_3$: $\text{Volume of } AlCl_3 \text{ solution} = \frac{\text{Moles of } AlCl_3 \text{ required}}{\text{Molarity of } AlCl_3} = \frac{0.2 \text{ mol}}{0.8 \text{ mol/L}} = 0.25 \text{ L}$ Converting to milliliters: $0.25 \text{ L} \times 1000 \text{ ml/L} = 250 \text{ ml}$