Question

Value of $\Lambda_m^\infty$ for $SrCl_2$ in water at $25^\circ$ from the following data:

Conc. (mol/L)	0.25	1
$\Lambda_m (\Omega^{-1} cm^2 mol^{-1})$	260	250

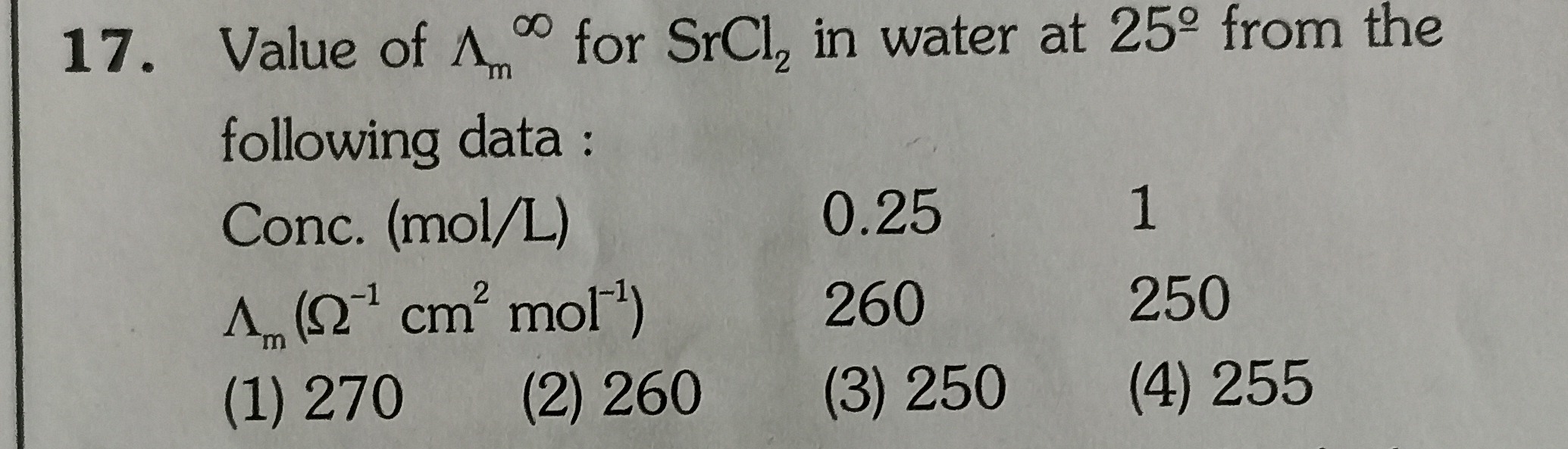
• A. 270
• B. 260
• C. 250
• D. 255

Answer 1

Answer: (A)

270

Answer 2

The problem asks for the molar conductivity at infinite dilution ($\Lambda_m^\infty$) for $SrCl_2$ using the provided experimental data. $SrCl_2$ is a strong electrolyte.

For strong electrolytes, the variation of molar conductivity ($\Lambda_m$) with concentration (C) can be described by the Debye-Hückel-Onsager equation:

$\Lambda_m = \Lambda_m^\infty - A\sqrt{C}$

where:

$\Lambda_m$ is the molar conductivity at concentration C.

$\Lambda_m^\infty$ is the molar conductivity at infinite dilution.

A is a constant for a given solvent and temperature, specific to the type of electrolyte.

We are given two data points:

1. When C = 0.25 mol/L, $\Lambda_m = 260 \, \Omega^{-1} cm^2 mol^{-1}$
2. When C = 1 mol/L, $\Lambda_m = 250 \, \Omega^{-1} cm^2 mol^{-1}$

Let's set up two equations using the Debye-Hückel-Onsager equation:

For the first data point ($C = 0.25$ mol/L):

$\sqrt{C} = \sqrt{0.25} = 0.5$

$260 = \Lambda_m^\infty - A(0.5)$ --- (1)

For the second data point ($C = 1$ mol/L):

$\sqrt{C} = \sqrt{1} = 1$

$250 = \Lambda_m^\infty - A(1)$ --- (2)

Now we have a system of two linear equations with two unknowns ($\Lambda_m^\infty$ and A).

Subtract Equation (2) from Equation (1):

$(260 - 250) = (\Lambda_m^\infty - 0.5A) - (\Lambda_m^\infty - A)$

$10 = \Lambda_m^\infty - 0.5A - \Lambda_m^\infty + A$

$10 = 0.5A$

$A = \frac{10}{0.5}$

$A = 20$

Now substitute the value of A back into Equation (2) to find $\Lambda_m^\infty$:

$250 = \Lambda_m^\infty - A$

$250 = \Lambda_m^\infty - 20$

$\Lambda_m^\infty = 250 + 20$

$\Lambda_m^\infty = 270 \, \Omega^{-1} cm^2 mol^{-1}$

Alternatively, using Equation (1):

$260 = \Lambda_m^\infty - 0.5A$

$260 = \Lambda_m^\infty - 0.5(20)$

$260 = \Lambda_m^\infty - 10$

$\Lambda_m^\infty = 260 + 10$

$\Lambda_m^\infty = 270 \, \Omega^{-1} cm^2 mol^{-1}$

Both methods yield the same result.

The value of $\Lambda_m^\infty$ for $SrCl_2$ is $270 \, \Omega^{-1} cm^2 mol^{-1}$.