Question

The joint equation of two lines passing through the origin and perpendicular to the lines given by $2x^2 + 5xy + 3y^2 = 0$ is

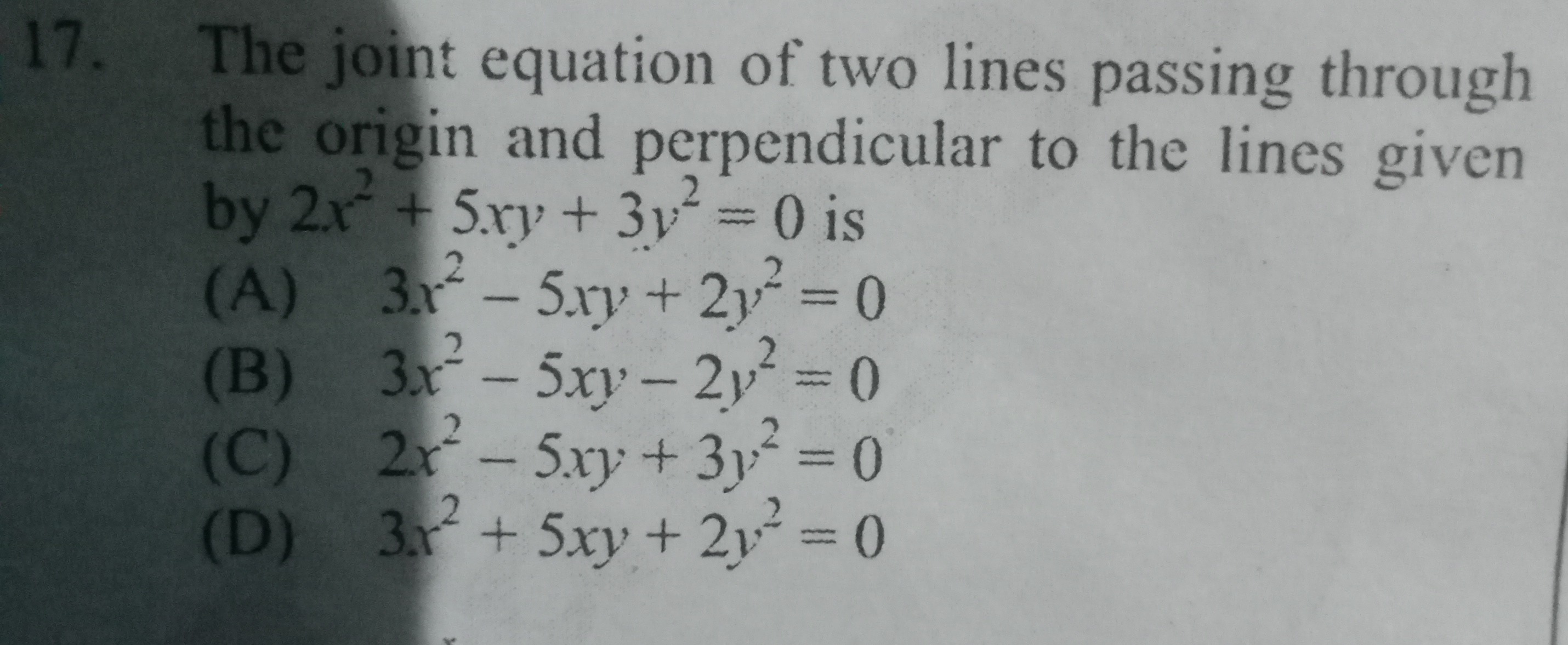
• A. $3x^2 - 5xy + 2y^2 = 0$
• B. $3x^2 - 5xy - 2y^2 = 0$
• C. $2x^2 - 5xy + 3y^2 = 0$
• D. $3x^2 + 5xy + 2y^2 = 0$

Answer 1

Answer: (A)

$3x^2 - 5xy + 2y^2 = 0$

Answer 2

The given equation $2x^2 + 5xy + 3y^2 = 0$ represents a pair of lines passing through the origin. For a general equation $ax^2 + 2hxy + by^2 = 0$, the joint equation of the pair of lines passing through the origin and perpendicular to these lines is $bx^2 - 2hxy + ay^2 = 0$. In the given equation, $a=2$, $2h=5$, and $b=3$. Substituting these values into the formula $bx^2 - 2hxy + ay^2 = 0$, we get $3x^2 - 5xy + 2y^2 = 0$.