Question

Let f(x) = [n + p sin x], x ∈ (0, π), n ∈ l and p is a prime number, where [.] denotes the greatest integer function. Then the number of points where f(x) is not differentiable, is:

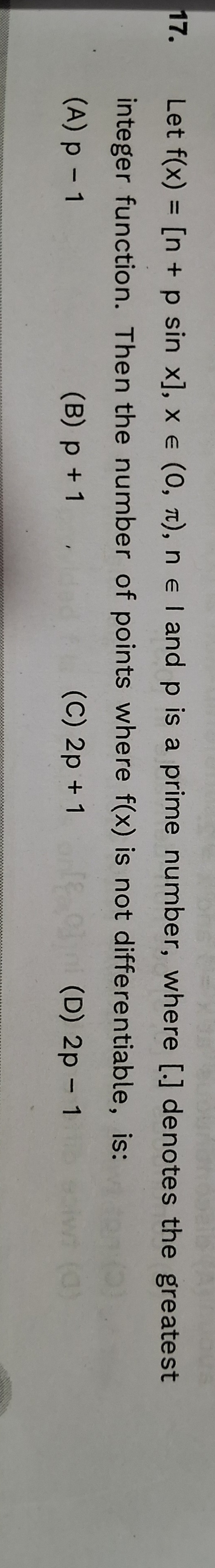
• A. p - 1
• B. p + 1
• C. 2p + 1
• D. 2p - 1

Answer 1

Answer: (D)

2p - 1

Answer 2

The function given is $f(x) = [n + p \sin x]$, where $x \in (0, \pi)$, $n \in \mathbb{Z}$, and $p$ is a prime number. We need to find the number of points where $f(x)$ is not differentiable.

The greatest integer function $[y]$ is not differentiable at points where $y$ is an integer. Let $g(x) = n + p \sin x$. The function $f(x) = [g(x)]$ is generally not differentiable when $g(x)$ is an integer. Since $n$ is an integer, $n + p \sin x$ will be an integer if and only if $p \sin x$ is an integer.

Let $k = p \sin x$, where $k$ is an integer.

1. Determine the range of $p \sin x$ for $x \in (0, \pi)$:
   For $x \in (0, \pi)$, the value of $\sin x$ ranges from values just above $0$ to $1$. Specifically, $\sin x \in (0, 1]$.
   Therefore, $p \sin x \in (0, p]$.

2. Identify possible integer values for $k$:
   The integer values $k$ that $p \sin x$ can take are $1, 2, 3, \dots, p$.

3. Solve for $x$ for each integer value of $k$:
   We need to solve $\sin x = \frac{k}{p}$ for $x \in (0, \pi)$.

   • Case 1: $k \in \{1, 2, \dots, p-1\}$
     For these values of $k$, we have $0 < \frac{k}{p} < 1$.
     For each such value of $\sin x$, there are two distinct solutions for $x$ in the interval $(0, \pi)$:
     $x_1 = \arcsin\left(\frac{k}{p}\right)$ and $x_2 = \pi - \arcsin\left(\frac{k}{p}\right)$.
     Since there are $(p-1)$ such values of $k$, this gives $2 \times (p-1)$ points where $p \sin x$ is an integer.

   • Case 2: $k = p$
     In this case, $\sin x = \frac{p}{p} = 1$.
     For $x \in (0, \pi)$, there is only one solution: $x = \frac{\pi}{2}$.
     This gives 1 point where $p \sin x$ is an integer.

   In total, there are $2(p-1) + 1 = 2p - 1$ points where $n + p \sin x$ is an integer.

4. Check differentiability at these points:
   A function $f(x) = [g(x)]$ is not differentiable at $x_0$ if $g(x_0)$ is an integer and $g'(x_0) \neq 0$. If $g'(x_0) = 0$, further analysis is required.
   Let $g(x) = n + p \sin x$. Then $g'(x) = p \cos x$.

   • For $x$ values from Case 1 ($\sin x = \frac{k}{p}$ where $k \in \{1, \dots, p-1\}$):
     At these points, $\sin x \neq 1$ and $\sin x \neq 0$. This implies $\cos x \neq 0$.
     Therefore, $g'(x) = p \cos x \neq 0$.
     At these $2(p-1)$ points, $f(x)$ has a jump discontinuity (as $g(x)$ crosses an integer value with a non-zero slope), and thus $f(x)$ is not differentiable.

   • For $x = \frac{\pi}{2}$ (from Case 2):
     At $x = \frac{\pi}{2}$, $g(\frac{\pi}{2}) = n + p \sin(\frac{\pi}{2}) = n+p$, which is an integer.
     Now, let's check $g'(\frac{\pi}{2}) = p \cos(\frac{\pi}{2}) = p \times 0 = 0$.
     Since $g'(\frac{\pi}{2}) = 0$, we need to examine the function's behavior around $x = \frac{\pi}{2}$.
     $g(x) = n + p \sin x$.
     For $x$ near $\frac{\pi}{2}$ (but $x \neq \frac{\pi}{2}$), $\sin x < 1$.
     Therefore, $n + p \sin x < n+p$.
     Since $n+p$ is an integer, for values of $x$ close to $\frac{\pi}{2}$ (but not equal to $\frac{\pi}{2}$), the value of $[n + p \sin x]$ will be $[n+p - \text{small positive number}] = n+p-1$.
     So, $f(x) = n+p-1$ for $x \neq \frac{\pi}{2}$ in a neighborhood of $\frac{\pi}{2}$.
     However, at $x = \frac{\pi}{2}$, $f(\frac{\pi}{2}) = [n+p] = n+p$.
     This shows that $f(x)$ has a jump discontinuity at $x = \frac{\pi}{2}$. A function with a jump discontinuity is not differentiable at that point.
     Thus, $x = \frac{\pi}{2}$ is also a point of non-differentiability.

5. Total number of points of non-differentiability:
   Combining both cases, the total number of points where $f(x)$ is not differentiable is $2(p-1) + 1 = 2p - 2 + 1 = 2p - 1$.