Solveeit Logo
Login

Question

Question: $\int \frac{\sin 2x}{1+\cos^4 x} dx$ is equal to...

∫sin⁡2x1+cos⁡4xdx\int \frac{\sin 2x}{1+\cos^4 x} dx is equal to

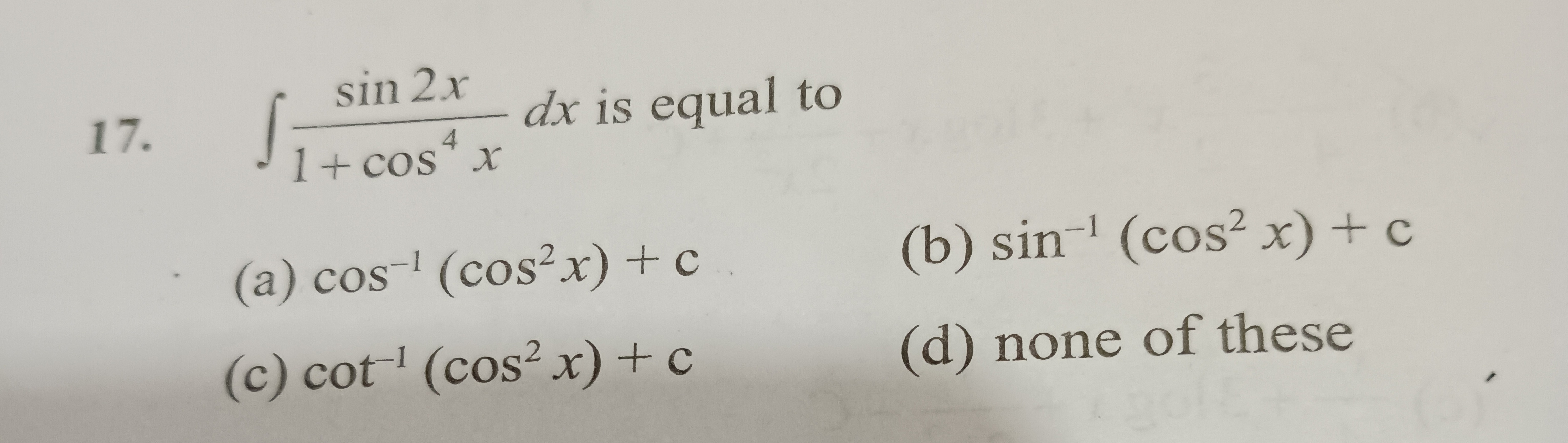
A

cos⁡−1(cos⁡2x)+c\cos^{-1}(\cos^2 x) + c

B

sin⁡−1(cos⁡2x)+c\sin^{-1}(\cos^2 x) + c

C

cot⁡−1(cos⁡2x)+c\cot^{-1}(\cos^2 x) + c

D

none of these

Answer

cot⁡−1(cos⁡2x)+c\cot^{-1}(\cos^2 x) + c

Explanation

Solution

To evaluate the integral ∫sin⁡2x1+cos⁡4xdx\int \frac{\sin 2x}{1+\cos^4 x} dx, we use the substitution method.

Let t=cos⁡2xt = \cos^2 x. Then, dtdx=−2sin⁡xcos⁡x=−sin⁡2x\frac{dt}{dx} = -2 \sin x \cos x = -\sin 2x. Thus, dt=−sin⁡2x dxdt = -\sin 2x \, dx.

The integral becomes:

I=∫−dt1+t2=−∫11+t2dt=−tan⁡−1(t)+C=−tan⁡−1(cos⁡2x)+CI = \int \frac{-dt}{1+t^2} = -\int \frac{1}{1+t^2} dt = -\tan^{-1}(t) + C = -\tan^{-1}(\cos^2 x) + C

Using the identity tan⁡−1(y)+cot⁡−1(y)=π2\tan^{-1}(y) + \cot^{-1}(y) = \frac{\pi}{2}, we can write −tan⁡−1(y)=cot⁡−1(y)−π2-\tan^{-1}(y) = \cot^{-1}(y) - \frac{\pi}{2}.

Therefore, I=cot⁡−1(cos⁡2x)−π2+CI = \cot^{-1}(\cos^2 x) - \frac{\pi}{2} + C.

Since CC is an arbitrary constant, we can absorb the term −π2-\frac{\pi}{2} into it, resulting in:

I=cot⁡−1(cos⁡2x)+C′I = \cot^{-1}(\cos^2 x) + C'

Thus, the correct answer is cot⁡−1(cos⁡2x)+c\cot^{-1}(\cos^2 x) + c.