Question

$\int \frac{sin 2x}{1+cos^4 x} dx$ is equal to

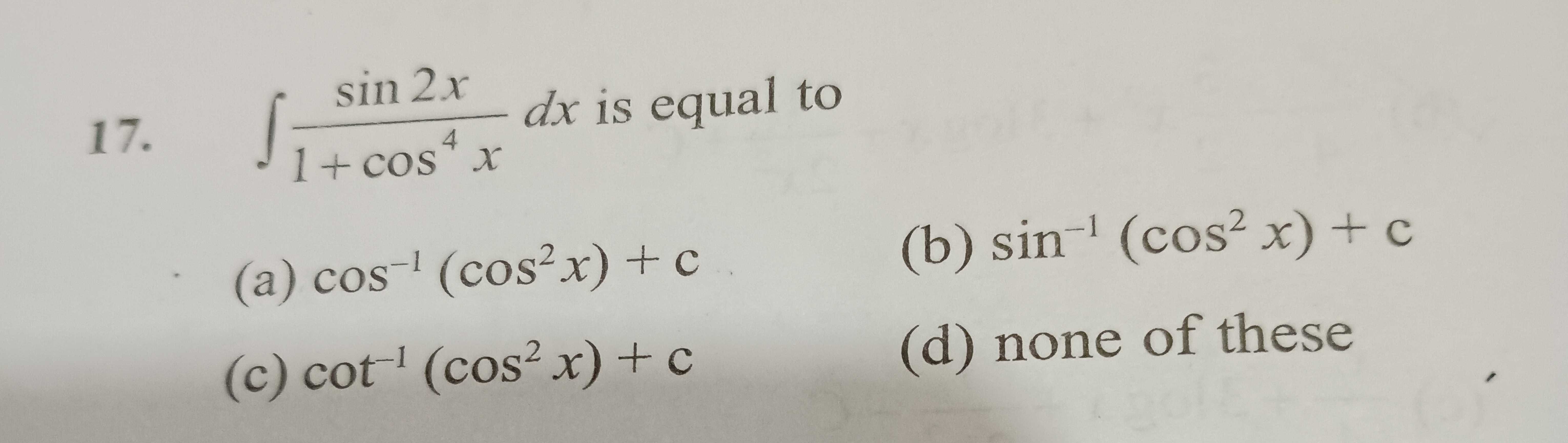
• A. $cos^{-1}(cos^2x) + c$
• B. $sin^{-1}(cos^2x) + c$
• C. $cot^{-1}(cos^2x) + c$
• D. none of these

Answer 1

Answer: (C)

$\cot^{-1} (\cos^2 x) + C'$

Answer 2

The problem asks us to evaluate the integral $\int \frac{\sin 2x}{1+\cos^4 x} dx$.

Let the given integral be $I$. $I = \int \frac{\sin 2x}{1+\cos^4 x} dx$

We can use the substitution method to solve this integral. Let $u = \cos^2 x$. To find $du$, we differentiate $u$ with respect to $x$: $\frac{du}{dx} = \frac{d}{dx}(\cos^2 x)$ Using the chain rule, $\frac{d}{dx}(f(x)^n) = n f(x)^{n-1} f'(x)$: $\frac{du}{dx} = 2 \cos x \cdot (-\sin x)$ $\frac{du}{dx} = -2 \sin x \cos x$ We know that $\sin 2x = 2 \sin x \cos x$. So, $\frac{du}{dx} = -\sin 2x$. This implies $du = -\sin 2x dx$. Therefore, $\sin 2x dx = -du$.

Now, substitute $u = \cos^2 x$ and $\sin 2x dx = -du$ into the integral: $I = \int \frac{-du}{1+u^2}$ $I = - \int \frac{1}{1+u^2} du$

We know the standard integral formula: $\int \frac{1}{1+x^2} dx = \tan^{-1} x + C$. Applying this formula: $I = -\tan^{-1} u + C$

Now, substitute back $u = \cos^2 x$: $I = -\tan^{-1} (\cos^2 x) + C$

We need to check if this result matches any of the given options. We know the trigonometric identity: $\tan^{-1} x + \cot^{-1} x = \frac{\pi}{2}$. From this identity, we can write $-\tan^{-1} x = \cot^{-1} x - \frac{\pi}{2}$. Applying this to our result: $I = \cot^{-1} (\cos^2 x) - \frac{\pi}{2} + C$ Since $C$ is an arbitrary constant of integration, the term $-\frac{\pi}{2} + C$ can be represented by a new arbitrary constant, say $C'$. $I = \cot^{-1} (\cos^2 x) + C'$

Comparing this with the given options: (a) $\cos^{-1}(\cos^2x) + c$ (b) $\sin^{-1}(\cos^2x) + c$ (c) $\cot^{-1}(\cos^2x) + c$ (d) none of these

Our result matches option (c).