Question

If $\overline{a} = i + 2j + 3k$, $b = -1 + 2j + k$, $c = 3i + j$ and $a + \lambda b$ is perpendicular to $c$, then $\lambda = \dots$

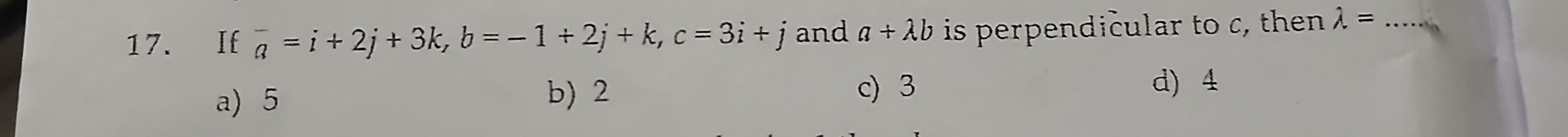
• A. 5
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (A)

5

Answer 2

Given vectors:

$$\mathbf{a} = i + 2j + 3k,\quad \mathbf{b} = -i + 2j + k,\quad \mathbf{c} = 3i + j$$

The vector $\mathbf{a} + \lambda \mathbf{b}$ is perpendicular to $\mathbf{c}$ if

$$(\mathbf{a} + \lambda \mathbf{b}) \cdot \mathbf{c} = 0.$$

First, calculate the dot product:

$$\mathbf{a} + \lambda \mathbf{b} = (1-\lambda,\;\;2+2\lambda,\;\;3+\lambda).$$

Since $\mathbf{c} = (3,1,0)$, we have:

$$(1-\lambda) \cdot 3 + (2+2\lambda) \cdot 1 + (3+\lambda) \cdot 0 = 0.$$

Simplify:

$$3(1-\lambda) + 2 + 2\lambda = 3 - 3\lambda + 2 + 2\lambda = 5 - \lambda = 0.$$

Thus,

$$\lambda = 5.$$