Question

Find the equation of the straight line which passes through the origin and makes angle 60° with the line $x + \sqrt{3} y + 3\sqrt{3} = 0$.

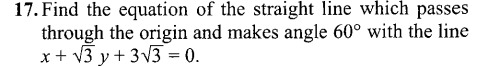
• A. x = 0 and x - \sqrt{3}y = 0
• B. y = 0 and x - \sqrt{3}y = 0
• C. x = 0 and x + \sqrt{3}y = 0
• D. y = 0 and x + \sqrt{3}y = 0

Answer 1

Answer: (A)

The equations of the straight lines are $x = 0$ and $x - \sqrt{3}y = 0$.

Answer 2

The given line $x + \sqrt{3} y + 3\sqrt{3} = 0$ has a slope $m_1 = -1/\sqrt{3}$, which corresponds to an angle $\theta_1 = 150^\circ$ with the positive x-axis. Let the required line make an angle $\theta$ with the positive x-axis. The angle between the two lines is given as $60^\circ$. Therefore, the angle $\theta$ must satisfy $|\theta - \theta_1| = 60^\circ$ or $|\theta - \theta_1| = 180^\circ - 60^\circ = 120^\circ$. Using $\theta_1 = 150^\circ$:

1. $\theta - 150^\circ = 60^\circ \implies \theta = 210^\circ$.
2. $\theta - 150^\circ = -60^\circ \implies \theta = 90^\circ$.
3. $\theta - 150^\circ = 120^\circ \implies \theta = 270^\circ$.
4. $\theta - 150^\circ = -120^\circ \implies \theta = 30^\circ$. The distinct angles are $90^\circ$ and $210^\circ$ (or $30^\circ$). A line passing through the origin with an angle of $90^\circ$ is a vertical line, $x=0$. A line passing through the origin with an angle of $210^\circ$ has a slope $m = \tan(210^\circ) = \tan(180^\circ + 30^\circ) = \tan(30^\circ) = 1/\sqrt{3}$. The equation is $y = (1/\sqrt{3})x$, which simplifies to $x - \sqrt{3}y = 0$.