Question

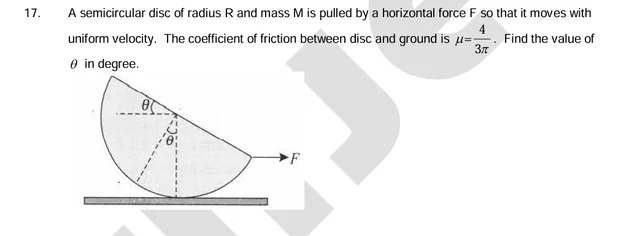
A semicircular disc of radius R and mass M is pulled by a horizontal force F so that it moves with uniform velocity. The coefficient of friction between disc and ground is $\mu = \frac{4}{3\pi}$. Find the value of $\theta$ in degree.

Answer 1

54

Answer 2

The problem describes a semicircular disc of radius R and mass M, pulled by a horizontal force F, moving with uniform velocity. The coefficient of friction between the disc and the ground is given as $\mu = \frac{4}{3\pi}$. We need to find the angle $\theta$ in degrees, which represents the tilt of the disc.

1. Force Analysis and Translational Equilibrium: Since the disc moves with uniform velocity, the net force acting on it is zero.

• Horizontal forces: The applied force F is balanced by the kinetic friction force $f$. $F - f = 0 \implies F = f$
• Vertical forces: The normal force N from the ground balances the gravitational force Mg. $N - Mg = 0 \implies N = Mg$

The friction force is given by $f = \mu N$. Substituting $N=Mg$, we get $f = \mu Mg$. Therefore, the applied force $F = \mu Mg$.

2. Center of Mass (CM) of a Semicircular Disc: The center of mass of a uniform semicircular disc of radius R is located at a distance $h_{CM}$ from the center of its flat base (which is also the center of the original full circle, let's call this point O). This distance is along the axis of symmetry (the line perpendicular to the flat base). $h_{CM} = \frac{4R}{3\pi}$

3. Torque Analysis and Rotational Equilibrium: For uniform velocity, the net torque acting on the disc must also be zero. We choose the point of contact (P) with the ground as the pivot point. The normal force (N) and friction force ($f$) pass through the pivot, so they produce no torque about P. The forces that produce torque about P are the applied force F and the gravitational force Mg.

• Torque due to applied force F ($\tau_F$): As shown in the diagram, the force F is applied horizontally at the center O (midpoint of the flat edge). The radius from O to the point of contact P makes an angle $\theta$ with the horizontal. The vertical height of the point O (where F is applied) above the pivot P is $y_O = R\sin\theta$. The torque due to F about P is $\tau_F = F \times y_O = F R\sin\theta$. This torque tends to rotate the disc clockwise.

• Torque due to gravitational force Mg ($\tau_{Mg}$): The gravitational force Mg acts vertically downwards through the center of mass (CM). The horizontal distance of the CM from the pivot P is $x_{CM}$. The CM is located at a distance $h_{CM}$ from O along the axis of symmetry. Since the radius OP makes an angle $\theta$ with the horizontal, the axis of symmetry (the line from O through CM) also makes an angle $\theta$ with the horizontal. The horizontal distance of O from P is $R\cos\theta$. The horizontal distance of CM from O (along the axis of symmetry) is $h_{CM}\cos\theta$. Since the CM is "below" O along the tilted axis (i.e., its horizontal position is closer to the vertical line passing through P than O's horizontal position), the horizontal distance of CM from P is $x_{CM} = R\cos\theta - h_{CM}\cos\theta = (R - h_{CM})\cos\theta$. The torque due to Mg about P is $\tau_{Mg} = Mg \times x_{CM} = Mg (R - h_{CM})\cos\theta$. This torque tends to rotate the disc counter-clockwise.

• Equating torques for equilibrium: For rotational equilibrium, the clockwise torque must balance the counter-clockwise torque: $\tau_F = \tau_{Mg}$ $F R\sin\theta = Mg (R - h_{CM})\cos\theta$

4. Substitute and Solve for $\theta$: Substitute $F = \mu Mg$ and $h_{CM} = \frac{4R}{3\pi}$ into the torque equation: $(\mu Mg) R\sin\theta = Mg \left(R - \frac{4R}{3\pi}\right)\cos\theta$ Divide both sides by $MgR$ (assuming $M, g, R$ are non-zero): $\mu \sin\theta = \left(1 - \frac{4}{3\pi}\right)\cos\theta$ Rearrange the equation to find $\tan\theta$: $\tan\theta = \frac{1 - \frac{4}{3\pi}}{\mu}$ $\tan\theta = \frac{\frac{3\pi - 4}{3\pi}}{\mu}$ Now, substitute the given value of $\mu = \frac{4}{3\pi}$: $\tan\theta = \frac{\frac{3\pi - 4}{3\pi}}{\frac{4}{3\pi}}$ $\tan\theta = \frac{3\pi - 4}{4}$

5. Calculate the numerical value of $\theta$: Using the approximate value of $\pi \approx 3.14159$: $\tan\theta = \frac{3 \times 3.14159 - 4}{4}$ $\tan\theta = \frac{9.42477 - 4}{4}$ $\tan\theta = \frac{5.42477}{4}$ $\tan\theta = 1.3561925$ To find $\theta$ in degrees, we take the inverse tangent: $\theta = \arctan(1.3561925)$ $\theta \approx 53.58^\circ$

Rounding to the nearest integer degree, $\theta \approx 54^\circ$.