Question

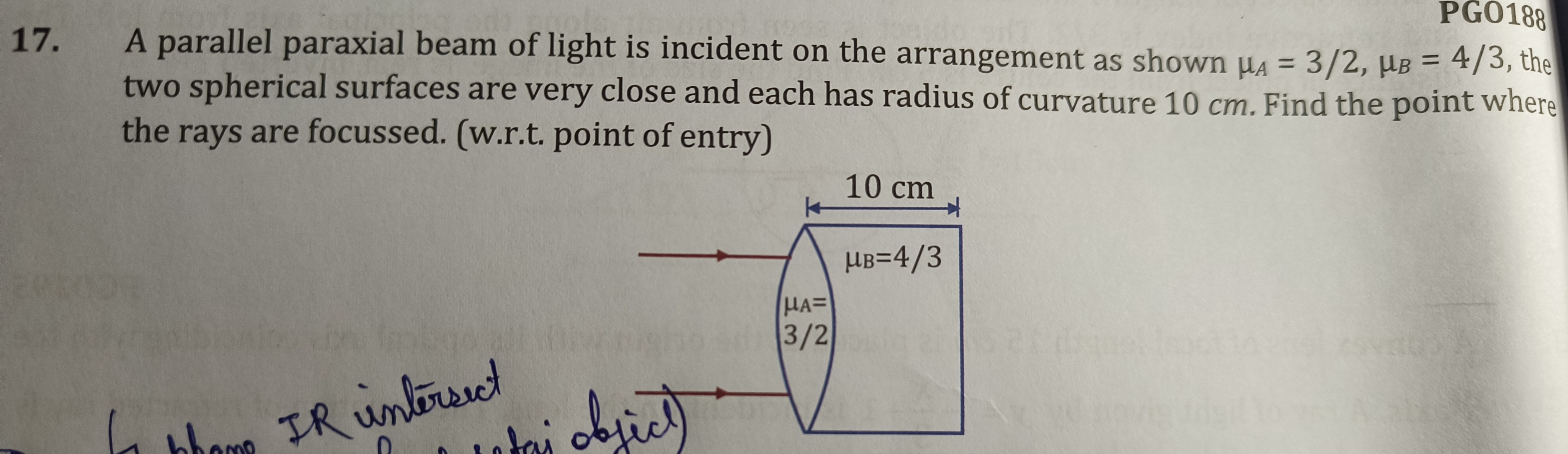
A parallel paraxial beam of light is incident on the arrangement as shown $\mu_A=3/2$, $\mu_B=4/3$, the two spherical surfaces are very close and each has radius of curvature $10$ cm. Find the point where the rays are focussed. (w.r.t. point of entry)

Answer 1

10 cm

Answer 2

The first part is a biconvex lens with $\mu_A = 3/2$ and radius of curvature $R = 10$ cm. Using the lens maker's formula: $\frac{1}{f_A} = (\mu_A - 1) \left(\frac{1}{R_1} - \frac{1}{R_2}\right)$ $\frac{1}{f_A} = \left(\frac{3}{2} - 1\right) \left(\frac{1}{10} - \frac{1}{-10}\right) = \frac{1}{2} \left(\frac{2}{10}\right) = \frac{1}{10} \text{ cm}^{-1}$ So, $f_A = 10$ cm. A parallel beam focuses at the focal length. The cylinder made of material B does not affect the focal point as it has parallel sides. Thus, the rays are focused at 10 cm from the point of entry.