Question
Question: $((\sqrt{2}-1)cosec \theta - sec \theta)cos3\theta$ at $\theta = \frac{\pi}{24}$ is-...
((2−1)cosecθ−secθ)cos3θ at θ=24π is-
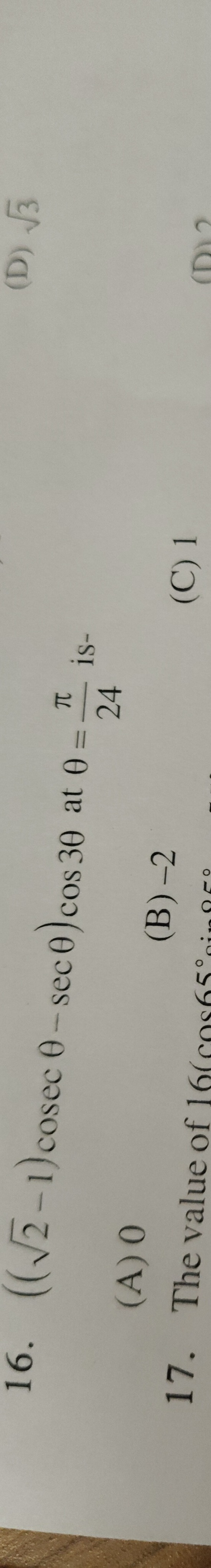
0
-2
1
3
The correct answer is 2, which is not present in the options. There might be an error in the question or options.
Solution
To evaluate the expression ((2−1)cosecθ−secθ)cos3θ at θ=24π, we proceed as follows:
- Substitute θ=24π into the expression.
- Simplify cos(3θ)=cos(243π)=cos(8π).
- Rewrite cosecθ as sinθ1 and secθ as cosθ1.
- Combine the terms inside the parenthesis: sinθcosθ(2−1)cosθ−sinθ.
- Recognize that 2−1=tan(8π).
- Substitute tan(8π) into the numerator and simplify using trigonometric identities, specifically the sine subtraction formula.
- Simplify the denominator using the double angle identity for sine.
- Cancel out common terms to arrive at the final result.
The step-by-step solution is as follows:
Given expression: ((2−1)cosecθ−secθ)cos3θ
Substitute θ=24π:
((2−1)cosec24π−sec24π)cos(3⋅24π)=((2−1)cosec24π−sec24π)cos(8π)
Rewrite in terms of sine and cosine:
(sin24π2−1−cos24π1)cos(8π)
Combine terms:
sin24πcos24π(2−1)cos24π−sin24πcos(8π)
Use 2−1=tan(8π):
sin24πcos24πtan(8π)cos24π−sin24πcos(8π)
Rewrite tan(8π) as cos(8π)sin(8π):
sin24πcos24πcos(8π)sin(8π)cos24π−sin24πcos(8π)
Simplify the numerator:
cos(8π)sin(8π)cos24π−cos(8π)sin24π⋅sin24πcos24π1cos(8π)
Using the sine subtraction formula sin(A−B)=sinAcosB−cosAsinB:
cos(8π)sin(8π−24π)⋅sin24πcos24π1cos(8π)
Simplify the angle: 8π−24π=243π−π=242π=12π:
cos(8π)sin(12π)⋅sin24πcos24π1cos(8π)
Using the double angle identity sin(2x)=2sinxcosx, we have sinxcosx=21sin(2x):
cos(8π)sin(12π)⋅21sin(12π)1cos(8π)
Simplify:
cos(8π)sin(12π)⋅sin(12π)2⋅cos(8π)
Cancel common terms:
2
Therefore, the value of the expression is 2, which is not among the given options. There may be an error in the question or the options provided.
