Question
Question: sin²x - cos 2x = 2 - sin 2x if...
sin²x - cos 2x = 2 - sin 2x if
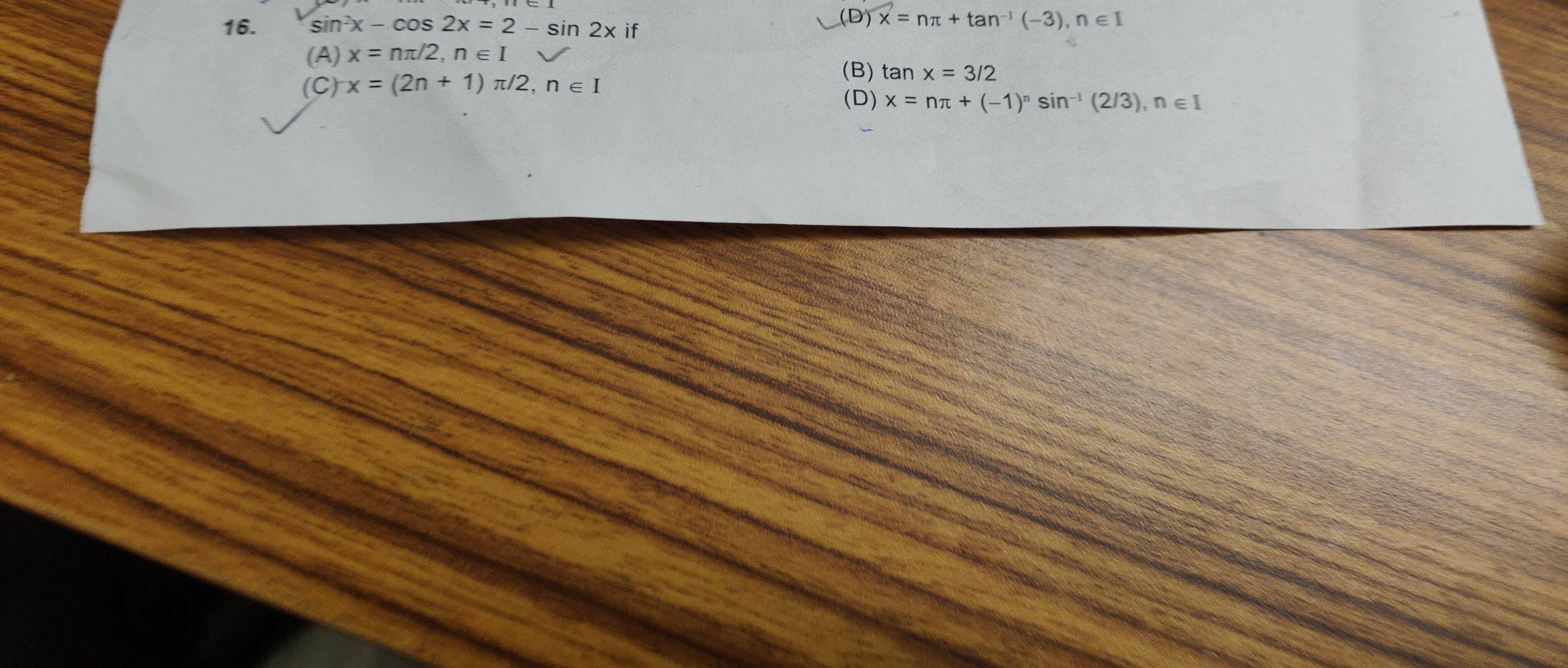
x = ηπ/2, η ∈ I
tan x = 3/2
x = (2n + 1) π/2, η ε Ι
x = ηπ + tan⁻¹ (-3), n ∈ 1
x = ηπ + (-1) sin⁻¹ (2/3), n ∈ 1
Options (B) and (C) are correct.
Solution
The given trigonometric equation is:
sin²x - cos 2x = 2 - sin 2x
We will use the following trigonometric identities to simplify the equation:
cos 2x = 1 - 2sin²xsin 2x = 2sin x cos xsin²x + cos²x = 1
Substitute the identities into the equation:
sin²x - (1 - 2sin²x) = 2 - (2sin x cos x)
sin²x - 1 + 2sin²x = 2 - 2sin x cos x
3sin²x - 1 = 2 - 2sin x cos x
Rearrange the terms to one side:
3sin²x + 2sin x cos x - 1 - 2 = 0
3sin²x + 2sin x cos x - 3 = 0
Now, substitute 3 with 3(sin²x + cos²x) using the identity sin²x + cos²x = 1:
3sin²x + 2sin x cos x - 3(sin²x + cos²x) = 0
3sin²x + 2sin x cos x - 3sin²x - 3cos²x = 0
The 3sin²x terms cancel out:
2sin x cos x - 3cos²x = 0
Factor out cos x:
cos x (2sin x - 3cos x) = 0
This equation holds true if either cos x = 0 or 2sin x - 3cos x = 0.
Case 1: cos x = 0
The general solution for cos x = 0 is x = (2n + 1)π/2, where n ∈ I (set of integers).
Let's verify this solution in the original equation:
If x = (2n + 1)π/2, then sin x = ±1, cos x = 0, sin 2x = 2sin x cos x = 0, and cos 2x = 2cos²x - 1 = 2(0)² - 1 = -1.
Substitute these into the original equation:
(±1)² - (-1) = 2 - 0
1 + 1 = 2
2 = 2
This is true. So, x = (2n + 1)π/2 is a valid solution. This matches option (C).
Case 2: 2sin x - 3cos x = 0
2sin x = 3cos x
If cos x = 0, then 2sin x = 0, which implies sin x = 0. However, sin x and cos x cannot both be zero for the same angle x. Therefore, cos x ≠ 0.
We can divide both sides by cos x:
2 (sin x / cos x) = 3
2 tan x = 3
tan x = 3/2
The general solution for tan x = 3/2 is x = nπ + tan⁻¹(3/2), where n ∈ I.
Let's verify this solution in the original equation:
If tan x = 3/2, we can find sin x and cos x. In a right-angled triangle, if tan x = 3/2, the opposite side is 3 and the adjacent side is 2. The hypotenuse is √(3² + 2²) = √13.
So, sin x = ±3/√13 and cos x = ±2/√13. (The signs of sin x and cos x must be the same since tan x > 0).
sin²x = (±3/√13)² = 9/13
sin 2x = 2sin x cos x = 2 (±3/√13)(±2/√13) = 2 (6/13) = 12/13
cos 2x = cos²x - sin²x = (±2/√13)² - (±3/√13)² = 4/13 - 9/13 = -5/13
Substitute these into the original equation:
9/13 - (-5/13) = 2 - 12/13
9/13 + 5/13 = (26 - 12)/13
14/13 = 14/13
This is true. So, tan x = 3/2 is a valid solution. This matches option (B).
Conclusion:
Both x = (2n + 1)π/2 and tan x = 3/2 are valid conditions for the given equation to hold true.
Let's check the given options:
(A) x = ηπ/2, η ∈ I: This includes x = nπ (even multiples of π/2), for which cos x = ±1 and sin x = 0. Substituting x = nπ into the original equation gives 0² - 1 = 2 - 0, which simplifies to -1 = 2, which is false. Therefore, option (A) is incorrect.
(B) tan x = 3/2: This is a correct solution.
(C) x = (2n + 1) π/2, η ε Ι: This is a correct solution.
(D) x = ηπ + tan⁻¹ (-3), n ∈ 1: This implies sin x = 2/3. If sin x = 2/3, then tan x = (2/3) / (±√(1 - (2/3)²)) = (2/3) / (±√5/3) = ±2/√5, which is not 3/2. Therefore, option (D) is incorrect.
Since both (B) and (C) are correct solutions to the equation, and assuming this is a multiple-choice question where multiple options can be correct, both (B) and (C) are the answers. If it is a single-choice question, there might be an ambiguity in the question itself.
