Question

$\lim_{x \to \infty} \left[ \frac{sinx}{x} \right]$

Answer 1

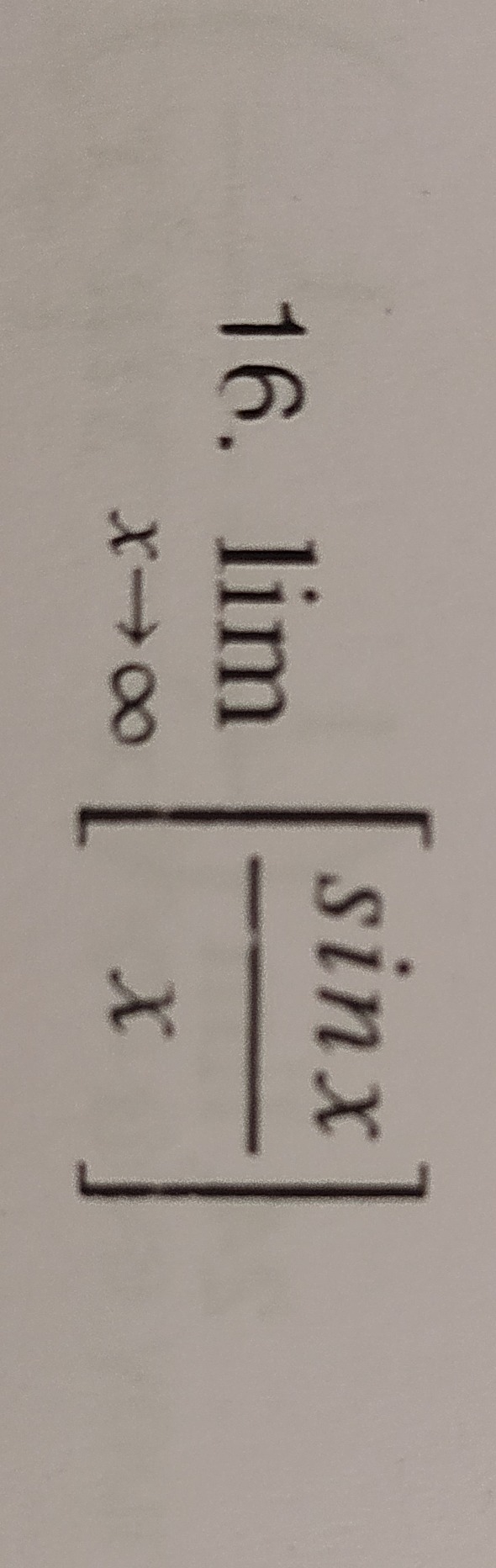
Does not exist

Answer 2

We are asked to find the limit $\lim_{x \to \infty} \left[ \frac{sinx}{x} \right]$, where $[y]$ denotes the greatest integer function of $y$.

First, let's analyze the behavior of the function inside the greatest integer function, $\frac{sinx}{x}$, as $x \to \infty$. We know that the sine function is bounded, i.e., $-1 \le sinx \le 1$ for all real $x$. For $x > 0$, we can divide the inequality by $x$: $\frac{-1}{x} \le \frac{sinx}{x} \le \frac{1}{x}$.

Now, let's evaluate the limits of the lower and upper bounds as $x \to \infty$: $\lim_{x \to \infty} \frac{-1}{x} = 0$ $\lim_{x \to \infty} \frac{1}{x} = 0$

By the Squeeze Theorem, since $\frac{sinx}{x}$ is bounded between $\frac{-1}{x}$ and $\frac{1}{x}$, and both bounds converge to 0 as $x \to \infty$, the function $\frac{sinx}{x}$ also converges to 0: $\lim_{x \to \infty} \frac{sinx}{x} = 0$.

Now, we need to evaluate the limit of the greatest integer function of $\frac{sinx}{x}$ as $x \to \infty$. Since $\lim_{x \to \infty} \frac{sinx}{x} = 0$, for sufficiently large values of $x$, the value of $\frac{sinx}{x}$ will be very close to 0.

Let's consider the values of $\frac{sinx}{x}$ for large $x$. For $x > 1$, we have $-1/x \le \frac{sinx}{x} \le 1/x$. As $x \to \infty$, the interval $[-1/x, 1/x]$ shrinks towards 0.

For very large $x$, the value of $\frac{sinx}{x}$ is a number close to 0. This number can be positive or negative depending on the sign of $sinx$. The sign of $sinx$ alternates as $x$ increases. $sinx > 0$ for $x \in (2n\pi, (2n+1)\pi)$ and $sinx < 0$ for $x \in ((2n+1)\pi, (2n+2)\pi)$ for integer $n$.

Consider large values of $x$ such that $sinx > 0$. For these values, $\frac{sinx}{x}$ is a small positive number. For sufficiently large $x$, $0 < \frac{sinx}{x} < 1$. The greatest integer of such a number is 0. For example, if $x$ is large and $sinx > 0$, $\frac{sinx}{x}$ could be 0.001, 0.0001, etc. The greatest integer $[0.001] = 0$, $[0.0001] = 0$.

Consider large values of $x$ such that $sinx < 0$. For these values, $\frac{sinx}{x}$ is a small negative number. For sufficiently large $x$, $-1 < \frac{sinx}{x} < 0$. The greatest integer of such a number is -1. For example, if $x$ is large and $sinx < 0$, $\frac{sinx}{x}$ could be -0.001, -0.0001, etc. The greatest integer $[-0.001] = -1$, $[-0.0001] = -1$.

As $x \to \infty$, $x$ passes through intervals where $sinx > 0$ and intervals where $sinx < 0$. In intervals where $sinx > 0$, for large $x$, $\left[ \frac{sinx}{x} \right] = 0$. In intervals where $sinx < 0$, for large $x$, $\left[ \frac{sinx}{x} \right] = -1$.

The function $\left[ \frac{sinx}{x} \right]$ oscillates between the values 0 and -1 for arbitrarily large values of $x$. For a limit to exist as $x \to \infty$, the function must approach a single value. Since $\left[ \frac{sinx}{x} \right]$ takes on two different values (0 and -1) infinitely often as $x \to \infty$, the limit does not exist.

For example, consider the sequence $x_n = 2n\pi + \pi/2$. As $n \to \infty$, $x_n \to \infty$. $\frac{sin(x_n)}{x_n} = \frac{sin(2n\pi + \pi/2)}{2n\pi + \pi/2} = \frac{sin(\pi/2)}{2n\pi + \pi/2} = \frac{1}{2n\pi + \pi/2}$. As $n \to \infty$, $\frac{1}{2n\pi + \pi/2} \to 0$. For large $n$, $0 < \frac{1}{2n\pi + \pi/2} < 1$. So, $\lim_{n \to \infty} \left[ \frac{sin(x_n)}{x_n} \right] = \lim_{n \to \infty} \left[ \frac{1}{2n\pi + \pi/2} \right] = [0] = 0$.

Consider the sequence $y_n = 2n\pi + 3\pi/2$. As $n \to \infty$, $y_n \to \infty$. $\frac{sin(y_n)}{y_n} = \frac{sin(2n\pi + 3\pi/2)}{2n\pi + 3\pi/2} = \frac{sin(3\pi/2)}{2n\pi + 3\pi/2} = \frac{-1}{2n\pi + 3\pi/2}$. As $n \to \infty$, $\frac{-1}{2n\pi + 3\pi/2} \to 0$. For large $n$, $-1 < \frac{-1}{2n\pi + 3\pi/2} < 0$. So, $\lim_{n \to \infty} \left[ \frac{sin(y_n)}{y_n} \right] = \lim_{n \to \infty} \left[ \frac{-1}{2n\pi + 3\pi/2} \right] = [-1] = -1$.

Since we found two sequences $x_n$ and $y_n$ both tending to infinity, but the limit of the function along these sequences is different (0 and -1), the limit $\lim_{x \to \infty} \left[ \frac{sinx}{x} \right]$ does not exist.