Question

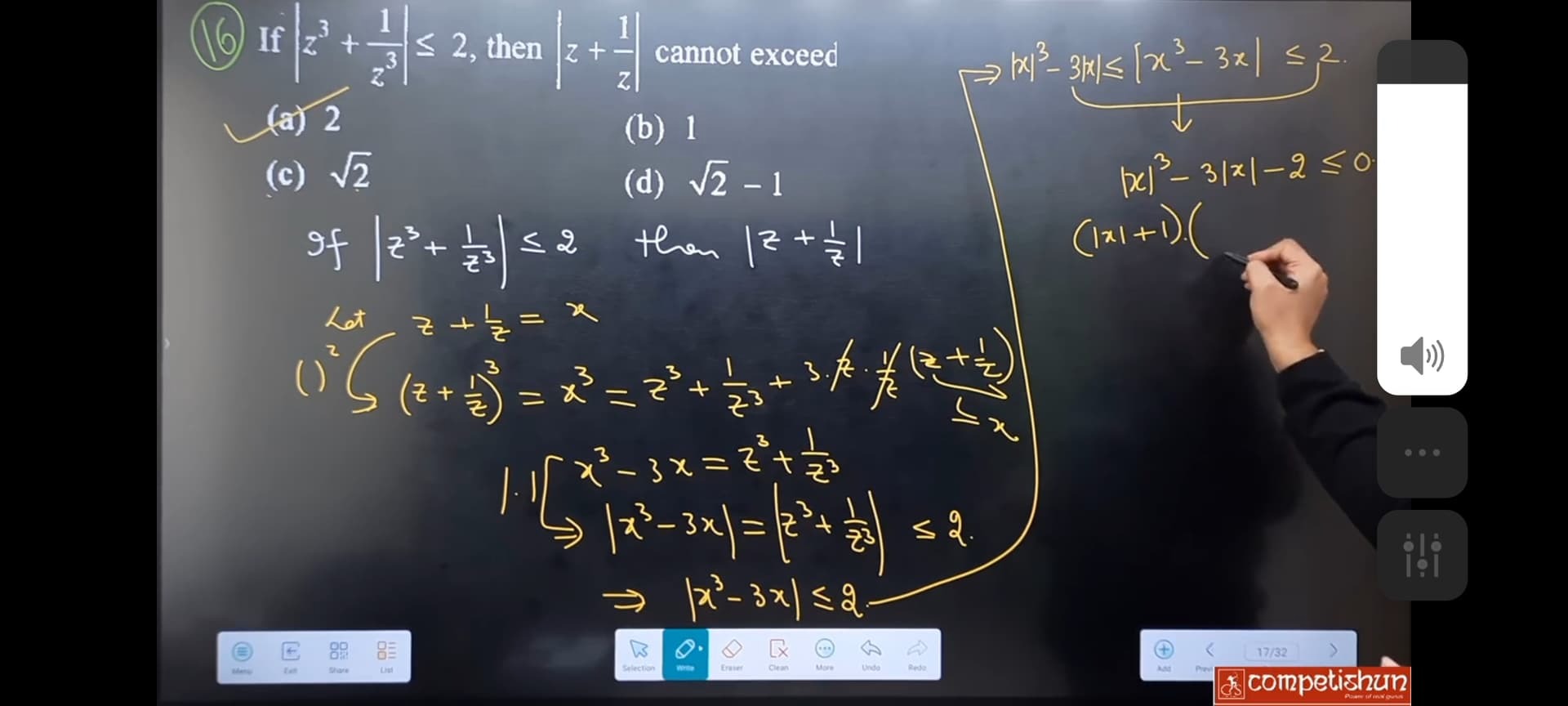
If $|z^3 + \frac{1}{z^3}| \leq 2$, then $|z + \frac{1}{z}|$ cannot exceed

• A. 2
• B. 1
• C. $\sqrt{2}$
• D. $\sqrt{2}-1$

Answer 1

Answer: (A)

2

Answer 2

To find the maximum value of $|z + \frac{1}{z}|$, given $|z^3 + \frac{1}{z^3}| \leq 2$.

Let $x = z + \frac{1}{z}$. We know the algebraic identity for cubes: $(a+b)^3 = a^3 + b^3 + 3ab(a+b)$. Applying this to $x$: $x^3 = \left(z + \frac{1}{z}\right)^3 = z^3 + \left(\frac{1}{z}\right)^3 + 3 \cdot z \cdot \frac{1}{z} \left(z + \frac{1}{z}\right)$ $x^3 = z^3 + \frac{1}{z^3} + 3x$ Rearranging the terms, we get an expression for $z^3 + \frac{1}{z^3}$ in terms of $x$: $z^3 + \frac{1}{z^3} = x^3 - 3x$

Now, substitute this into the given inequality: $|x^3 - 3x| \leq 2$

We use the reverse triangle inequality property: $||A| - |B|| \leq |A - B|$. Let $A = x^3$ and $B = 3x$. Then $||x^3| - |3x|| \leq |x^3 - 3x|$. This implies $||x|^3 - 3|x|| \leq |x^3 - 3x|$. Since we are given $|x^3 - 3x| \leq 2$, we can write: $||x|^3 - 3|x|| \leq 2$

Let $y = |x|$. Since $|x|$ represents a magnitude, $y \geq 0$. The inequality becomes $|y^3 - 3y| \leq 2$. This means $-2 \leq y^3 - 3y \leq 2$. We need to solve two inequalities:

1. $y^3 - 3y \leq 2 \implies y^3 - 3y - 2 \leq 0$
2. $y^3 - 3y \geq -2 \implies y^3 - 3y + 2 \geq 0$

Let's solve the first inequality: $y^3 - 3y - 2 \leq 0$. We look for integer roots of the polynomial $P(y) = y^3 - 3y - 2$. By inspection, if $y = -1$, $P(-1) = (-1)^3 - 3(-1) - 2 = -1 + 3 - 2 = 0$. So, $(y+1)$ is a factor. We perform polynomial division or synthetic division: $(y^3 - 3y - 2) \div (y+1) = y^2 - y - 2$. Now, factor the quadratic $y^2 - y - 2$: $(y-2)(y+1)$. So, $y^3 - 3y - 2 = (y+1)(y-2)(y+1) = (y+1)^2(y-2)$. The inequality becomes $(y+1)^2(y-2) \leq 0$. Since $y = |x|$, we know $y \geq 0$. For $y \geq 0$, $(y+1)$ is always positive (in fact, $y+1 \geq 1$), so $(y+1)^2$ is always positive (in fact, $(y+1)^2 \geq 1$). For the product $(y+1)^2(y-2)$ to be less than or equal to zero, the term $(y-2)$ must be less than or equal to zero. So, $y-2 \leq 0 \implies y \leq 2$.

Now let's solve the second inequality: $y^3 - 3y + 2 \geq 0$. We look for integer roots of the polynomial $Q(y) = y^3 - 3y + 2$. By inspection, if $y = 1$, $Q(1) = (1)^3 - 3(1) + 2 = 1 - 3 + 2 = 0$. So, $(y-1)$ is a factor. We perform polynomial division: $(y^3 - 3y + 2) \div (y-1) = y^2 + y - 2$. Now, factor the quadratic $y^2 + y - 2$: $(y+2)(y-1)$. So, $y^3 - 3y + 2 = (y-1)(y+2)(y-1) = (y-1)^2(y+2)$. The inequality becomes $(y-1)^2(y+2) \geq 0$. Since $y = |x|$, we know $y \geq 0$. For $y \geq 0$, $(y-1)^2$ is always non-negative. Also, for $y \geq 0$, $(y+2)$ is always positive (in fact, $y+2 \geq 2$). Since both $(y-1)^2$ and $(y+2)$ are non-negative for $y \geq 0$, their product $(y-1)^2(y+2)$ will always be non-negative. So, this inequality is always true for $y \geq 0$.

Combining the results from both inequalities: We have $y \leq 2$ from the first inequality, and $y \geq 0$ (since $y = |x|$). The second inequality provides no further restriction on $y$ for $y \geq 0$. Thus, $0 \leq y \leq 2$. Substituting back $y = |x|$, we get $0 \leq |x| \leq 2$. Since $x = z + \frac{1}{z}$, we have $0 \leq |z + \frac{1}{z}| \leq 2$. Therefore, $|z + \frac{1}{z}|$ cannot exceed 2.